Randomization은 어떻게 인과를 추론할 수 있도록 할까?

Home About

Causal Inference

허석영

May 31, 2022

5 min

네오가 파란 약을 먹었다면, 행복했을까?

이 글은 제 개인블로그에서도 읽으실 수 있어요

영화 ‘매트릭스’에서 네오는 진실을 볼 수 있도록 하는 빨간 약과, 허구 속에서 살도록 하는 파란약 사이에서 선택할 것을 요구 받습니다. 네오는 진실을 마주하고 매트릭스에서 나오기 위해 빨간 약을 선택합니다. 그런데 빨간 약이라는 선택(treatment)는 네오를 더욱 행복하게(outcome) 만들었을까요? 이는 빨간 약 선택(D)-네오의 행복(Y)이라는 두 변인의 인과를 알도록 하는 인과추론의 문제와 연결됩니다. 문제를 풀기 위해서, 인과추론의 전제가 무엇인지 그리고 잠재적 결과 프레임워크가 무엇인지, 나아가 무작위 배정이 인과효과 파악에 어떻게 기여하는지 순차적으로 알아보도록 할게요.

인과추론의 제1전제 ceteris paribus

인과적 해석을 위한 제 1전제는, 다른 조건이 동일하다면(other thing equal, ceteris paribus) 입니다. ceteris paribus가 충족되었을 때, 우리는 특정 개입(intervention)과 결과(outcome)의 인과관계를 명확하게 알 수 있습니다. 인과추론에 대해 상세하게 설명한 책 “고수들의 계량경제학”에서 나오는 다양한 방법론 IV, DID, PSM, RD 등도 모두 ceteris paribus를 충족하기 위한 방법론이라 할 수 있습니다. 오늘 다룰 주제, randomization(무작위 배정) 또한 그렇습니다.

다시 매트릭스로 돌아와 볼게요. 빨간 약과 행복의 인과관계를 알기 위해서는, 빨간 약이라는 선택(treatment)을 제외한 다양한 변인을 통제(control)하여 ceteris paribus를 만들어야 합니다. 간단한 방법은, 빨간 약과 파란 약을 각각 먹고 그 삶을 살아낸 다음 행복지수를 측정하는 것입니다. 빨간 약을 먹었을 때의 행복과 파란 약을 먹었을 때의 행복의 차이를 계산하여, 빨간 약의 효과를 파악하는 것이죠.(네…?)

잠재적 결과 프레임워크(Potential Outcome Framework)

무슨… 우리가 닥터 스트레인지도 아니고 어떻게 그럴 수 있어요? 라고 질문하실 줄 알고 닥터 스트레인지를 모시고 왔습니다. 오늘 모신 닥터는 시간을 다루는 능력도 뛰어나지만, 인과추론에 도움을 주는 프레임워크, 즉 잠재적 결과 프레임워크(Potential Outcome Framework)에 대해서도 조예가 깊다고 하는데요.(?) 잠재적 결과 프레임워크는 잠재적 결과 간의 차이를 통해 인과를 해석할 수 있도록 하는 프레임워크입니다.

먼저 개인 단위부터 수식을 통해서 하나씩 짚어보도록 할게요. 개인은, 특정 처치(treatment)에 대해서 2가지 잠재적 결과(potential outcome)와 1가지 실제 결과(actual outcome)를 가질 수 있어요. $Y_i^1$ 은 빨간 약을 먹었을 때의 행복을 의미하고, $Y_i^0$ 은 파란 약을 먹었을 때의 행복을 의미합니다. 그리고 $Y_i$ 는 선택에 따라 도출된 실제 결과입니다.

potential \: outcomes - treatment: \: Y^1_i \: (red-pill)\\ potential \: outcomes - untreatment: \: Y^0_i \: (blue-pill) \\ actual \: outcomes : \: Y_i

잠재적 결과와 실제 결과는 그 행위 여부(D)에 따라 아래와 같은 관계를 가집니다. $D_i = 1$ 은 처치를 한 것(빨간약을 먹은 것)이고, $D_i = 0$ 은 처치를 하지 않은 것(파란 약을 먹은 것)인데요. 만약 $D_i = 1$ 이라면 (1) 수식 우측항의 오른쪽이 소거되어 $Y_i^1$ 라는 잠재적 결과가 실제 결과가 되고, $D_i = 0$ 이라는 수식 우측항의 왼쪽이 소거되어 $Y_i^0$ 이라는 잠재적 결과가 실제 결과가 됩니다.

Y_i = D_iY^1_i + (1-D_i)Y^0_i \\ if \; D_i = 1 \; then \; Y_i=Y^1_i \\ if \; D_i = 0 \; then \; Y_i=Y^0_i \\

그리고 우리가 그토록 알고 싶어하는, 빨간 약과 행복의 인과관계는 잠재적 결과의 차이를 통해 알 수 있습니다. delta( $\delta_i$ )가 양수이며 크다면, 우리는 빨간 약이라는 선택이 행복에 기여할 수 있다고 판단할 수 있는 것이죠. 우리 곁에 닥터 스트레인지가 있다면, 우리는 각 선택의 잠재적 결과를 선제적으로 파악하고 그에 따라 빨간 약 혹은 파란 약이라는 최적의 선택을 하면 됩니다.(?)

\delta_i = Y^1_i-Y^0_i

빨간 약, 파란 약 테스트

그러나 닥터 스트레인지는 바쁘고, 저희가 검증해야 할 사람은 많습니다. 매번 타임스톤을 통해 잠재적 결과의 차이를 구하는 것은, 너무 번거롭고 공수가 많이 드는 일이죠. 그래서 한번만 더 닥터의 힘을 빌려, 인과추론의 메커니즘을 명확히 파악하고, 이를 활용해 집단 단위에서 빨간 약과 행복의 인과관계를 파악해보려고 합니다.

이를 위해 매트릭스 세상에서 10명의 사람을 데려왔습니다. 각 사람의 잠재적 결과를 파악해서, 각 선택(빨간 약/파란 약)이 그 사람에 행복에 얼마나 기여하는지 측정했습니다. 그 결과 5명은 빨간 약이 행복에 기여했고( $\delta > 0$ ), 다른 5명은 파란 약이 행복에 기여했다는 것( $\delta < 0$ )을 발견할 수 있었습니다.

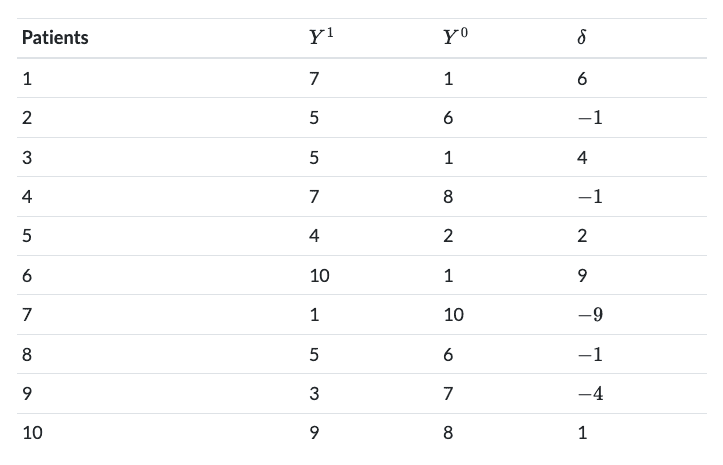
또한, 각 잠재적 결과를 명확하게 알 수 있었기에 빨간 약이라는 선택이 행복이라는 결과에 평균적으로 얼마나 기여하는지도 계산할 수 있습니다. 평균적 처치 효과(ATE, Average Treatment Effect)는 각 개인의 $\delta$ (잠재적 결과의 차이)의 평균 값입니다. 아래 수식에 따라 전개해보면, 빨간 약이 평균적으로 0.6 만큼 더 행복에 기여한다는 것을 발견할 수 있습니다.

\begin{aligned} ATE &= E[\delta_i] \\ &= E[Y^1_i - Y^0_i] \\ &= E[Y^1_i] - E[Y^0_i] \\ &= 5.6 - 5 \\ &= 0.6 \end{aligned}

닥터는 면밀한 분석을 위해 약-행복 기여도에 따라, 빨간 약이 행복에 기여하는 집단 A( $D_i = 1$ )와 파란 약이 행복에 기여하는 집단 B( $D_i = 0$ )로 나눴습니다. 그리고 각 집단에 빨간 약이 기여하는 정도를 추가로 확인했죠. 그리고 빨간 약이 평균적으로 집단 A에 끼치는 처치 효과(ATT, Average Treatment Effect for the Treatment group)는 4.4이라는 것, 빨간 약이 평균적으로 집단 B에 끼치는 처치 효과(ATU, Average Treatment Effect for the Un-treatment group)는 -3.2라는 것도 발견했습니다. ATT와 ATU의 가중 평균은 ATE와 동일하기도 합니다.

\begin{aligned} ATT & = E\big[\delta_i\mid D_i=1\big] \\ & = E\big[Y^1_i - Y^0_i \mid D_i = 1\big] \\ &= (6+4+2+9+1) / 5 = 4.4 \end{aligned}

\begin{aligned} ATU &= E\big[\delta_i\mid D_i = 0\big] \\ &= E\big[Y^1_i - Y^0_i\mid D_i = 0\big] \\ &= (-1-1-9-1-4)/5 = -3.2 \end{aligned}

섬세한 닥터는 모든 사람의 행복을 위해, 빨간 약과 파란 약 중 각 사람의 행복에 최대한 기여하도록 약을 처방했습니다. 그 결과, $\delta$ 값에 따라서, 사람들은 아래와 같이 빨간 약/파란 약을 처방 받게 되었습니다.

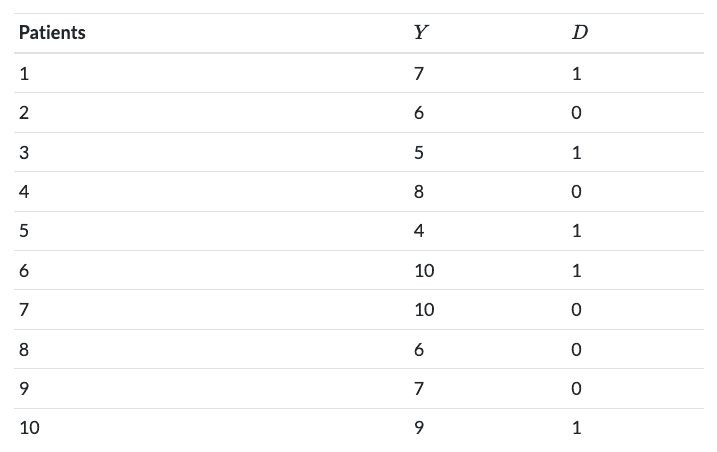
뿌듯해하며 퇴근하려던 순간, 지나가던 행인이 “어라, 빨간 약을 먹은 사람들이 덜 행복하네요.”라고 합니다. 실제로 집단A와 집단B의 행복지수 실제 결과 차이(SDO, Simple Difference in Outcomes)를 확인해보니, 집단A가 -0.4 만큼 덜 행복하다는 것이 발견되었습니다.

\begin{aligned} SDO &=E\big[Y^1\mid D=1\big] - E\big[Y^0\mid D=0\big] \\ &= (7 + 5 + 4 + 10 + 9) / 5 - (6 + 8 + 10 + 6 + 7) / 5 \\ &= 7 - 7.4 \\ &= -0.4 \end{aligned}

닥터는 뭔가 이상한 점을 느끼고, SDO를 3가지 요소로 분해했습니다. 그리고 SDO는 ATE와 2가지 bias의 합으로 구성되었다는 것을 발견했습니다. 정리하면, 인과효과가 있어도(ATE > 0)로 나온다고 해도, Selection bias와 Heterogeneous treatment effect bias에 따라, 실제 결과는 좋지 않게 나올 수 있는 것이죠.(SDO < 0)

\begin{aligned} \underbrace{\dfrac{1}{N_T} \sum_{i=1}^n \big(y_i\mid d_i=1\big)-\dfrac{1}{N_C} \sum_{i=1}^n \big(y_i\mid d_i=0\big)}_{ \text{Simple Difference in Outcomes}} &= \underbrace{E[Y^1] - E[Y^0]}_{ \text{Average Treatment Effect}} \\ &+ \underbrace{E\big[Y^0\mid D=1\big] - E\big[Y^0\mid D=0\big]}_{ \text{Selection bias}} \\ & + \underbrace{(1-\pi)(ATT - ATU)}_{ \text{Heterogeneous treatment effect bias}} \end{aligned}

실제로 그러한지, 각 bias를 계산해보도록 할게요. Selection bias는 집단A(D=1)와 집단B(D=0)가 처치를 받지 않았을 때의 결과 차이를 의미합니다. 다시 말해, 집단A, 집단B 모두 파란 약을 먹었을 때(매트릭스 세계에 남아있었을 때)의 행복지수의 차이를 말하는 것이죠. 계산해보니, 두 집단은 빨간 약, 파란 약 투약 여부와 관계없이 행복지수의 차이가 -4.8만큼 존재했다는 것을 발견할 수 있었습니다.

\begin{aligned} \underbrace{E\big[Y^0\mid D=1\big] - E\big[Y^0\mid D=0\big]}_{ \text{Selection bias}} &=(1+1+2+1+8) / 5 - (6+8+10+6+7) / 5 \\ &= -4.8 \end{aligned}

다음으로 Heterogeneous treatment effect bias를 계산해봤습니다. Heterogeneous treatment effect bias는 처치(treatment)가 두 집단에 끼치는 효과의 차이를 의미합니다. 동일한 처치가, 집단에 따라 다른 효과가 있는지 보려는 것이죠. 계산해보니, 빨간 약 투약의 효과가 3.8 만큼 차이가 나고 있었네요.

\begin{aligned} \underbrace{(1-\pi)(ATT - ATU)}_{ \text{Heterogeneous treatment effect bias}} &= 0.5 * (4.4 - (-3.2)) = 3.8 \end{aligned}

정리하면, 빨간 약은 사람들의 행복에 효과가 있지만(ATE=0.6) 그 효과는 사람들의 기본 행복지수 차이(Selection bias=-4.8)와 빨간 약 투약 효과의 차이(Heterogeneous treatment effect bias=3.8)로 인해, 오히려 효과가 없는 것처럼 보이게 된 것이었죠.(SDO=-0.4) 지금까지의 과정을 통해 실제 결과(SDO)에서 bias를 제거하면 순수한 인과효과(ATE)를 추론할 수 있다는 것을 깨달았습니다. 그러나 bias는 잠재적 결과(counterfactual)을 알아야만 계산할 수 있기에, 닥터의 도움 없이는 bias도 나아가 ATE도 계산할 수 없습니다. 잠재적 결과를 딱 알지 못하더라도, ATE를 추정할 수 있는 방법은 없을까요?

무작위 배정, 타임스톤만큼 강력한 것

\begin{align} E\big[Y^1\mid D=1\big] - E\big[Y^1\mid D=0\big]=0 \: (red-pill) \\ E\big[Y^0\mid D=1\big] - E\big[Y^0\mid D=0\big]=0 \: (blue-pill) \end{align}

닥터의 도움 없이 빨간 약의 효과를 추론하는 방법은, 무작위 배정(randomization assignment)입니다. 우리는 무작위 배정을 통해, 각 bias를 순차적으로 제거할 수 있는데요. 잠재적 결과와 상관없이 집단 A,B를 나눈다면, 다음과 같은 수식을 도출할 수 있습니다. 무작위로 배정했기에, 빨간약을 먹었을 때의 집단 A,B의 평균적 행복은 별반 다르지 않을 거라(0일 것이다) 생각할 수 있는 것이지요.(1) 이는 파란약을 먹었을 때도 마찬가지일 테고요.(2) 집단A, B의 파란 약을 먹었을 때의 평균적 행복이 다르지 않다면, 우리는 이를 통해 Selection bias를 소거할 수 있습니다.

\begin{align} \underbrace{E\big[Y^0\mid D=1\big] - E\big[Y^0\mid D=0\big]}_{ \text{Selection bias}} &= 0 \: (blue-pill) \end{align}

남은 것은 Heterogeneous treatment effect bias입니다. 이 또한, 위 수식(2)을 활용하여 아래와 같이 소거할 수 있습니다. ATT - ATU 수식은, (1)수식에서 (2)수식을 뺀 수식인데요, (1)(2)수식이 0이 됨에 따라, $ATT - ATU$ 수식도 0이 되고, 그 결과 Heterogeneous treatment effect bias도 0이 된다는 것을 알 수 있습니다. 정리하면, 무작위 배정을 통해 집단A,B를 충분히 무작위로 나눈다면 각 bias를 충분히 줄여, 실제 결과 차이(SDO)만으로 잠재적 결과 차이를, 즉 인과의 효과(ATE)를 추론할 수 있게 됩니다.

\begin{align} ATT = E\big[Y^1\mid D=1\big] - E\big[Y^0\mid D=1\big] \\ ATU = E\big[Y^1\mid D=0\big] - E\big[Y^0\mid D=0\big] \end{align}

\begin{align} ATT-ATU & =\mathbf{E\big[Y^1\mid D=1\big]}-E\big[Y^0\mid D=1\big] \\ & - \mathbf{E\big[Y^1 \mid D=0\big]}+ E\big[Y^0\mid D=0\big] \\ & = 0 \\ \end{align}

\begin{align} \underbrace{(1-\pi)(ATT - ATU)}_{ \text{Heterogeneous treatment effect bias}} &= 0 \end{align}

“This kind of randomization of the treatment assignment would eliminate both the selection bias and the heterogeneous treatment effect bias.” - causal inference, mixtape

영화 ‘매트릭스’에서 네오라는 ‘개인’이 빨간 약을 먹었을 때 행복할지, 사실 우리는 알 수 없습니다. 시간을 되돌릴 수 없기 때문이죠. 다만, 무작위 배정이라는 방법을 통해서, 매트릭스 사람들이라는 ‘집단’이 빨간 약을 먹었을 때 행복할지는 어느 정도 추정할 수 있습니다. 빨간 약이라는 개입(intervention) 외 요소를 통제하여 각 bias를 제거함으로써, 실제 결과 차이로 잠재적 결과 차이를 추론할 수 있는 방법, randomization을 활용한다면 말이죠 :)