이 글은 넷플릭스 블로그에서 A/B Testing과 그 활용에 대해 소개한 글 시리즈 중 하나입니다. 그 중에서도 통계적인 개념을 설명하는 부분이 Part 3,4인데요. 앞서 박찬민님께서 Part3에 대해 정리해주셔서, 이어지는 Part 4에 대해 정리해보고자 합니다.

우리는 앞선 글에서 실험 결과를 해석할 때 나타나는 두 가지 오류에 대해 정의했습니다. False Positive(거짓 양성), False Negative(거짓 음성). 그리고 우리는 이 개념과 함께 통계적 유의성, P-Value, 신뢰구간에 대한 이해를 위해 동전 던지기를 활용했습니다. 이 글에서는, 동전 던지기를 활용해서 거짓 음성과 통계적 검정력에 대해 이해해보고자 합니다.

False Negatives and Power

거짓 음성은 실제로는 차이가 있지만, 데이터가 처리군과 대조군 사이의 유의미한 차이를 나타내지 않을 때 발생합니다. Part 3에서의 예와 이어서, 거짓 음성은 고양이 사진을 고양이가 아닌 것으로 판단합니다. “거짓 양성은 통계적 개념에서의 검정력과 깊은 연관이 있습니다. 이 검정력은 실험 환경에서 참 양성을 발견한 확률을 의미합니다. 사실 이 검정력은 거짓 음성 비율을 1에서 뺀 것과 동일합니다.

검정력은 실제 세상에 대한 가정에서 발생할 수 있는 결과들과 관련이 있습니다. Part3에서 우리가 유의성을 정의할 때 귀무가설이 참이라는 가정에서 출발한 것과 같은 맥락입니다. 검정력에 대해 이해하기 위해, Part3에서 활용했던 동전 뒤집기로 돌아가 봅시다. 우리의 목표는 동전을 100번 던지는 실험에서 앞면이 얼마나 나오는지를 계산하는 실험을 통해 동전이 공정한지를 보는 것이었습니다. 동전이 공정하다는 귀무가설 하에서 결과의 분포는 밑에 있는 그림의 검은 영역입니다. 그림을 이해하기 위해, 우리는 Histogram을 평활화했습니다.

만약 이 동전이 공정하지 않은 동전이라면 어떻게 될까요? 우리의 동전이 평균적으로 앞면이 나올 확률이 64%라고 가정해봅시다. 우리의 실험에는 불확실성이나 노이즈가 존재하기 때문에, 동전을 100번 뒤집었을 때 앞면이 정확히 64번 나오지는 않을 것입니다. 하지만 동전이 공정하다는 귀무가설 하에서, 대립가설이 사실이라면 발생할 수 있는 모든 경우의 수에 대해 계산할 수 있습니다. 그 분포는 밑에 있는 그림의 붉은 영역에 해당합니다.

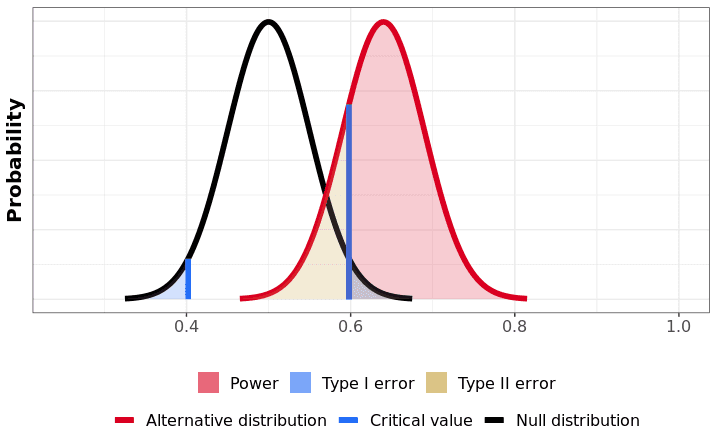
시각적으로, 검정력은 귀무가설 하에서 임계값 밖에 존재하는 붉은 분포의 비율입니다. 여기서, 붉은 분포의 80%는 임계값 밖에 존재하는, 즉 기각역에 있음을 볼 수 있습니다. 윗면이 나올 확률이 64%가 실제 사실이라는 가정 하에서, 이 실험의 검정력은 80%입니다. 보완하자면, 붉은 분포에서 무시할 수 있을 정도로 작은 일부분은 기각역보다 작은, 즉 채택역 내에 존재합니다.

검정력은 특정하고, 가정된 효과 크기에 해당합니다. 우리의 실험에서, 동전 던지기의 앞면이 나올 확률이 64%였다면, 그 동전이 공정하지 않다는 것을 밝혀낼 확률이 80%였습니다. 해석하자면, 동전의 앞면이 나올 확률이 64%인 동전으로 100번씩 던지는 실험을 여러 번 반복해서 유의수준 5%에서 의사결정을 했고, 5번의 실험 중 동전이 공정하다는 귀무가설을 4번 기각했습니다. 이 반복된 실험의 20%는 거짓 음성의 결과를 가집니다. 동전이 공정하지 않더라도, 공정하다는 귀무가설을 기각할 수 없을 것입니다.

Ways to increase Power

A/B Test를 설계함에 있어서, 우리는 유의 수준을 설정하고, (일반적으로 5%를 사용하지만, 실험군과 대조군 사이에 차이가 없다면, 전체 실험 중에서 5% 정도에서는 거짓 양성 결과가 나타날 것입니다.) 거짓 음성을 통제하기 위한 실험을 설계합니다.

1. 효과 크기(Effect Size)

쉽게 설명해서, 효과 크기가 커지면, (Group A와 B의 지표 차이가 커지면) 그 차이를 발견한 확률도 커집니다. 동전이 공정한지에 대한 실험을 한다고 해봅시다. 우리는 동전을 100번 던져서 앞면이 나오는 비율에 대한 데이터를 수집합니다. 여기서 두 가지의 시나리오를 생각해봅시다. 첫째, 실제 앞면이 나올 확률은 55%, 둘째, 실제 앞면이 나올 확률은 75%. 우리의 실험은 두 번째 실험에서 동전이 불공정하다는 것을 밝혀낼 확률이 높아보입니다. 실제로 앞면이 나올 확률이 귀무가설의 50%에서 떨어져 있기 때문에, 실험 결과가 기각역에 떨어질 확률이 높아보입니다. 효과 크기를 증가시키는 또 다른 전략은 프로덕트의 새로운 영역에서 실험하는 것입니다. 새로운 곳에서 고객들의 만족을 크게 증가시킬 여지가 존재할 수도 있기 때문이죠. 말하자면, 실험을 통해 얻어지는 즐거움 중 하나는 바로 놀라움입니다. 사소한 차이처럼 보일 지라도, 지표에는 엄청나게 큰 차이를 불러올 수도 있습니다.

2. 표본 크기(Sample size)

실험의 단위가 커지면, 검정력은 커지고 작은 차이를 정확하게 찾아내는 것이 쉬워집니다. 동전 실험으로 다시 돌아가서, 우리가 수집하는 데이터는 고정된 횟수의 동전 던지기에서 앞면이 나오는 횟수이고, 실제 앞면이 나올 확률은 64%입니다. 두 개의 시나리오를 생각해봅시다. 한 시나리오에서는 동전을 20번을, 다른 시나리오에서는 동전을 100번 던집니다. 직관적으로 생각하면 두 번째 실험에서 동전이 불공정하다는 결과가 나올 것 같습니다. 데이터가 많으면, 실험의 결과는 실제 64%에 가까워지고, 공정한 동전일 때 앞면이 나올 확률은 50% 이지만 기각역이 그 절반을 잠식하게 됩니다. 종합하면, 데이터가 많아지면 공정하지 않은 동전을 통한 실험의 결과가 기각역에 떨어질 확률이 높아지고, 참 양성이 되는 것입니다. 제품 개발 측면에서, 우리는 더 많은 표본을 수집하거나 테스트 그룹의 수를 줄임으로서 검정력을 증가시킬 수 있습니다. 물론 각 실험의 표본 크기와 중복되지 않는 실험의 Trade Off는 존재합니다.

3. 집단 내 지표의 변동성(The Variability of the metric in the underlying population)

우리가 실험하는 집단의 지표 동질성이 높을 수록, 실제 효과를 정확하게 발견할 확률이 높습니다. 넷플릭스에서 지연 시간을 줄이기 위한 실험을 한다고 해봅시다. 플레이 버튼을 누르고, 영상이 재생되기까지 걸리는 시간을 예로 들 수 있죠. 넷플릭스에 접속하는 사람들의 기기와 인터넷 환경이 다 다르다는 것을 고려하면, 유저들 사이에서 다양한 지표가 나타날 것입니다. 만약 실험처리가 지연 시간을 줄이는데 작은 영향을 미친다면, 유저들 사이에 존재하는 Noise들이 그 작은 영향(신호)을 잡아먹을 것입니다. 반대로, 만약 비슷한 기기와 인터넷 환경에서 서비스를 사용하는 유저들을 대상으로 실험을 한다면, 작은 영향(신호)도 찾아내기 쉬울 것입니다. 넷플릭스에서도 이 취약점을 활용하고, 실험환경의 다양성을 줄여서 검정력을 증가시키는 방향의 통계적 분석들을 설계해왔습니다.

Powering for reasonable and meaningful effects

검정력과 거짓 음성률은 가정된 효과크기의 역할을 합니다. 5%의 거짓 양성률이 폭넓게 받아들여지는 만큼, 합리적이고 유의미한 효과크기를 위해 80% 정도의 검정력을 목표로 하는 것이 일반적입니다. 효과크기를 가정하고 나서 실험을 설계하기 때문에, 만약 실제 처치효과가 우리가 가정한 것과 비슷하다면, 우리의 실험은 전체의 80% 정도에서 그 효과를 찾아낼 수 있을 것입니다. 반대로 20%에서는 거짓 음성 결과를 계산할 것입니다. 실제 효과가 있더라도 우리의 관측치는 기각역에 존재하지 않고, 효과가 있다는 결론을 내릴 수 없는 것입니다. 이것이 우리가 위에서 활용한 동전 뒤집기 예시에서 64%의 앞면 확률을 활용한 이유입니다.

합리적인 효과크기를 구성하는 것은 좀 까다로울 수 있습니다. 하지만 도메인 지식과 상식을 활용해서 단단한 가정을 할 수 있습니다. 유저들이 적절한 컨텐츠를 선택할 수 있도록 하는 추천시스템을 최적화하는 것과 같은 분야에서 넷플릭스는 오랫동안 실험을 해왔습니다. 여ㅜ기서 실험이 만드는 긍/부정적인 효과크기에 대해 단단한 경험을 쌓아왔습니다. 이러한 경험을 바탕으로, 우리의 실험이 80% 정도의 검정력을 가질 수 있도록 표본을 구성할 수 있습니다.

두 번째 고려사항은 실험을 설계하는 것과 자원을 투자할 곳을 찾는 것에서, 의사결정에 필요한 주요 지표에 유의미한 영향을 미치는 것이 무엇인가를 결정하는 것입니다. 유의미함은 실험이 영향을 미치는 영역(고객 만족도, 재생 지연시간, 백엔드 시스템의 기술적 성능 등등이 있겠죠. )과 프로덕트 경험과 연관되는 자원이나 비용에 따라 달라질 것입니다. 효과크기가 지표를 0.1% 이하로 변화시킨다고 가정하면, 소요되는 비용이 이익보다 더 큰 상황이 발생합니다. 이 경우에, 지표의 0.01%의 차이를 찾는 실험에 큰 의미가 없습니다. 성공적으로 효과를 찾는 것이 의사결정에 유의미한 기여를 하지 않을 것이기 때문입니다. 비슷하게, 실험의 효과크기가 유저 경험이나 비즈니스에 그다지 중요하지 않은 영역이라면, 실험에 투자할 자원을 다른 곳에서 더 효율적으로 사용할 수 있을 것입니다.

Summary

이 시리즈의 Part 3,4는 실험 결과를 해석하는데 필요한 경험들에 대해 소개했습니다. 거짓 양성(False Positives), 거짓 음성(False Negatives), 통계적 유의성(Statistical Significance), P-Value, 검정력(Power)

실험의 불편한 진실은 우리가 거짓 양성과 거짓 음성을 동시에 줄일 수는 없다는 것입니다. 사실, 거짓 양성과 거짓 음성은 모순적인 관계(Trade Off)를 가집니다. 우리가 거짓 양성률을 0.01%과 같이 그럴 듯한 수치를 사용한다면, A와 B에 차이가 없는 실험의 거짓 양성률을 줄이고자 할 것입니다. 하지만 동시에 검정력이 낮아지고, 거짓 음성률은 증가합니다. 5%의 거짓 양성률을 사용하고 80%의 검정력을 목표로 한다면, 거짓의 발견을 제한하고 참을 발견하는 것 사이의 균형을 유지할 수 있습니다. 그러나, 거짓 양성이나 거짓 음성이 큰 리스크를 갖는 경우에, 연구자들은 불확실성을 줄일

우리의 목표는 불확실성을 제거하는 것이 아니라, 의사결정을 위해 불확실성을 이해하고 정량화하는 것입니다. 많은 경우에, A/B Test는 미묘한 해석이 필요하고, 이는 비즈니스의 의사결정에 필요한 하나의 입력값일 뿐입니다. 다음 글에서, 이 실험 결과를 활용해서 명확한 의사결정을 내리는 방법에 대해 소개하고자 합니다.