A/B 테스트의 확장판, MAB (Multi-Armed Bandits) 알고리즘

Home About

Experiment

이은지

November 03, 2021

7 min

이번 포스팅에서는 A/B 테스트의 확장판이라 볼 수 있는 MAB (Multi-Armed Bandits) 알고리즘에 대해 살펴보고, 이를 R 로 구현해보고자 합니다.
자세하게 구현할 알고리즘은 그리디 (Greedy), 입실론-그리디 (Epsilon-Greedy), UCB (Upper Confidence Bound), 톰슨 샘플링 (Thompson Sampling)입니다.
원 글은 이 링크에서 확인하실 수 있습니다.

A/B 테스트는 항상 어렵다

“A, B, C안 중 어떤게 가장 좋은 성과를 얻을 수 있을까?”

기업에선 위와 같이 항상 여러 가지 가능성을 열어두고 가장 좋은 선택이 무엇인지 고민하고 결정하는 의사 결정 과정을 거칩니다. 이에 대한 답을 얻는 가장 확실한 방법은 특정 기간 동안 고객마다 A, B, C안 중 랜덤하게 하나만 노출해서 가장 좋은 성과를 가지는 안을 선택하는 것입니다. 이것이 A/B 테스트의 기본적 컨셉입니다. 즉, A/B 테스트는 메뉴, 문구, 광고 등 고객마다 A안과 B안을 (내지는 C안까지) 다르게 보여주고 가장 반응이 좋은 안을 선택하는 방법입니다.

그러나 A/B 테스트에는 탐색(Exploration)과 활용 (Exploitation)의 문제가 존재합니다.

탐색 (Exploration)의 문제: “아 이럴 줄 알았으면 테스트 안 했지…”

테스트를 하면 할수록 기회 비용이 발생합니다.

예를 들어, 모 회사 직원 이모 씨는 배너에 A, B 문구 중 어떤 문구를 노출했을 때 매출액이 더 높은지 분석해달라는 요청을 받습니다. 이모 씨는 직관적으로 봤을 때 A 문구가 매출액이 높을 것이라 예상했지만, 이를 증명하기 위해 A/B 테스트를 시행했습니다. 고객들을 1:1 비율로 나누어 일주일 간 한 쪽은 A 문구만, 다른 한 쪽은 B 문구만 노출했습니다. 예상했듯이 A 문구가 매출액이 1,000만 원 더 높았습니다.

이 모씨는 테스트가 끝난 후 이런 생각을 하게 됩니다. “아, 이럴 줄 알았으면 테스트 안 했지… “. 테스트를 하지 않고 직관대로 처음부터 A 문구만 노출했다면 1,000만 원을 더 벌었을텐데 테스트를 하다보니 덜 벌었다 생각할 수 있는 것이죠.

활용(Exploitation)의 문제: “얼마나 더 해야 해?”

반대로, 테스트를 짧게 한다 해도 문제는 존재합니다.

앞에서 봤던 그 “이모 씨”는 시간이 없으니까 일주일만 A/B 테스트를 시행하라는 요청을 받습니다. 일주일 뒤에 결과를 봤더니 A안이 좋다는 결과가 나와 보고했더니 상사가 “이거 믿을 수 있는 결과야?”라 반박합니다. 이모씨는 할 말을 잃죠. (…)

이렇듯, 테스트를 짧게 하면 할수록 결과를 빨리 활용할 수 있기 때문에 더 많은 수익을 얻을 수 있지만, 통계라는게 표본이 작아질수록 결과의 신뢰성을 보장할 수 없습니다. 테스트 기간이 짧아지면 A안과 B안 중에 잘못된 안을 고를 수도 있습니다.

이를 방지하기 위해 테스트 기간은 “적당히” 길어야 합니다. 그러나 언제나 그렇듯 “적당히”의 기준은 주관적입니다. 대체적으로 실험 기간을 설정할 떄는 최소한의 비즈니스 사이클을 포함하도록 합니다. 주말의 매출이 크기 때문에 최소한 주말을 포함하도록 하고, 계절성을 고려해 테스트 기간을 정한다고는 하지만, 여전히 기간 설정에 따라 결과가 바뀔 수 있는 문제는 존재합니다.

이렇게 테스트에는 탐색 - 활용 교환 (Exploration - Exploitation tradeoff)이 존재합니다. 탐색 (Exploration)은 가장 나은 대안을 찾기 위해 테스트하는 과정을 의미하고, 활용 (Exploitation)은 테스트를 중단하고 결정된 대안을 선택하는 것을 의미합니다. 테스트를 많이 하면 많이 하는대로 기회 비용 문제가 발생하고, 안하면 안하는대로 신뢰성의 문제가 발생합니다. 이러한 문제를 체계화한 것이 MAB (Multi Armed Bandit) 문제입니다.

MAB가 왜 똑똑한가

MAB (Multi Armed Bandit)를 번역하면 “여러 팔 강도”입니다. 갑자기 웬 강도 (?)라 생각이 드실 수도 있지만, 이는 여러 대 슬롯 머신을 비유한 표현입니다. 영어에서 속어로 슬롯 머신을 “One Armed Bandit” (한 팔 강도)라 부르는데요. 실제로 구글링을 해보니 이런 슬롯 머신들이 검색이 되네요.

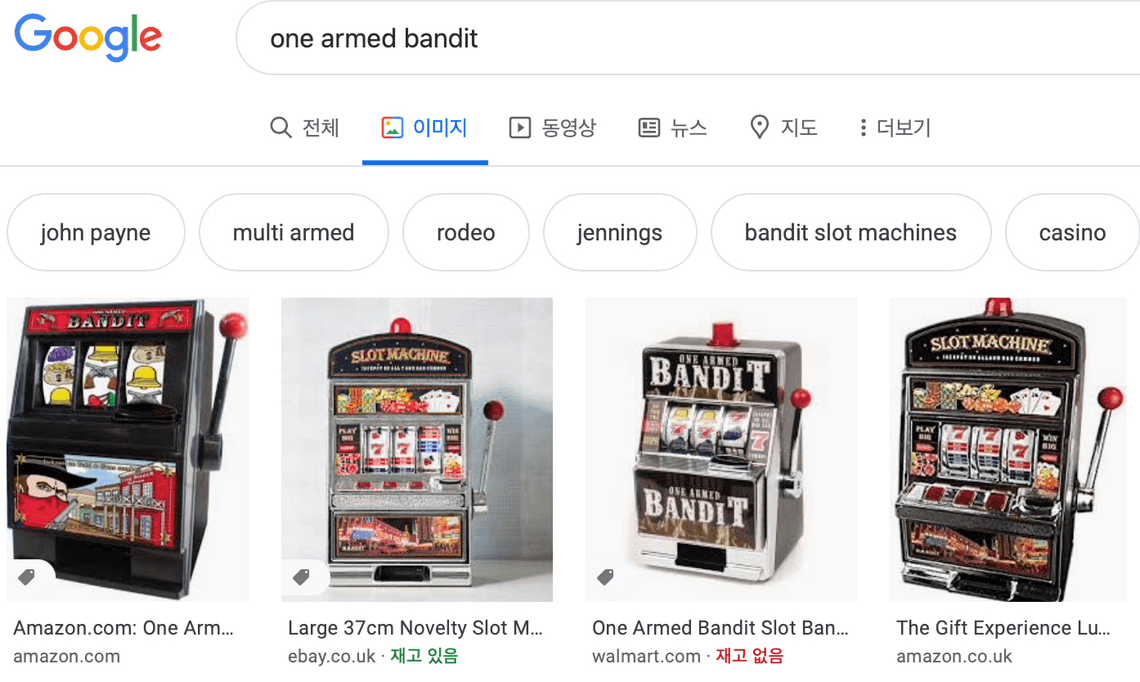
mab slotmachine

어감에서 느껴지듯이 슬롯머신이 오른 팔 하나만 가지고 도박객의 돈을 털어간다는 데에서 “한 팔 강도”라 표현한 것 같습니다.

다시 본론으로 돌아와서, MAB 알고리즘은 “Multi”이기 때문에 슬롯 머신이 여러 대 있는 상황입니다. 카지노에서는 슬롯 머신마다 돈을 따고 잃을 확률을 다르게 설정해둔다 합니다. 그럼 고객 입장에서 어떻게 하면 가장 높은 확률을 가진 슬롯머신을 택할 수 있을까요?

이에 대한 답에서도 “탐색-활용 교환”의 논리가 적용됩니다. 어느 슬롯머신의 수익률이 가장 좋은지 확인하려면 모든 슬롯 머신을 여러 번 당겨보면 되지만 그만큼 많은 돈이 필요합니다 (탐색). 이와 반대로 한 두 번씩만 당겨봐서 가장 수익률이 높은 슬롯머신을 택한다 해도 이게 가장 수익률이 높은 슬롯머신이라 단정하기 어렵습니다 (활용).

MAB가 똑똑한 이유는 이 탐색과 활용을 최적화하여, 매번 수익률이 높을 것으로 예상되는 슬롯머신을 선택해, 수익률을 극대화하기 때문입니다.

이런 MAB는 여러 분야에서 활용 가능합니다. 개인적으로 가장 와닿은건 “시간에 따라 수익률 프로파일이 달라지고 있는 상황에서 어떤 주식 옵션이 최고의 수익률을 줄 것인가?”인데요, MAB로 실제 주식의 이익을 최대화할 수 있다면 엄청나겠네요…~~해볼까~~

MAB에 쓰이는 용어

본론으로 들어가기 전에, MAB에 필요한 용어들을 정리해봅시다.

행동 (Action): MAB에서 선택된 대안 (ex. A/B 테스트에서 A안, B안)
보상 (Reward): 한 번의 행동에 따른 수치화된 결과 (ex. 클릭, 구매)
가치 (Value): 행동으로 인한 기대 보상

MAB에서는 모든 행동이 순서대로 발생한다 가정합니다. 그 순서에 따라 시점 $t$ 의 행동을 $A_t$ 라 하고, 행동에 따른 보상은 $R_t$ 로 표기합니다. 또한, 행동 $a$ 의 가치는 $q_*(a)$ , 시점 $t$ 에 추정된 가치는 $Q_t(a)$ 라 씁니다.

MAB에 쓰이는 네 개의 알고리즘

우리가 살펴볼 알고리즘은

그리디 (Greedy)
입실론-그리디 (Epsilon-Greedy)
UCB (Upper Confidence Bound)
톰슨 샘플링 (Thompson Sampling)

입니다. 이에 대한 코드는 [link]이 분의 코드를 많이 참조했습니다.

그리디 (Greedy) 알고리즘

한 번씩 해보고, 가장 많이 돈을 딴 슬롯머신 선택

MAB 알고리즘 중 가장 간단한 알고리즘은 그리디 알고리즘입니다. 예를 들어, 하루에 삼전, 네이비, 삼풍 주식을 샀는데 삼전에선 천원을 잃고, 네이비에서는 4천원을 벌고, 삼풍에서는 100만 원을 벌었다 가정합시다. 한 개미가 삼풍이 수익률이 가장 좋기 때문에 풀매수를 한다 할 때, 이 것이 바로 그리디 알고리즘의 컨셉입니다(이 예시는 실제 상황과 무관하며 지어낸 예시입니다 ^^;).

mab ant 출처: [link] {:.figure}

수식으로 풀자면 다음과 같습니다.

A_t = argmax_a Q_t(a)

현재 시점 $t$ 까지 기대 보상 $Q_t(a)$ , $a =$ {삼전, 네이비, 삼풍}를 최대화하는 행동 $A_t$ = 삼풍을 선택합니다. 이랬을 때 결과는 아시다시피, 떡락^{주식이 급락하는 것}의 위험성을 배제할 수 없습니다. 이처럼 그리디 알고리즘은 탐색 (Exploration)을 충분히 하지 않고, 활용 (Exploitation)을 너무 많이 하는 알고리즘입니다.

이를 R로 구현하면 다음과 같습니다.

저희가 고려할 주식은 삼전, 네이비, 삼풍이고, 이 주식들의 모평균과 표준 편차를 다음과 같이 정의했습니다.

삼전은 하루에 평균적으로 4천원 이익을 가져다주고, 5천원의 표준편차를 가집니다.
네이비는 하루에 평균적으로 3천원의 이익을 가져다주고, 만 원의 표준편차를 가집니다.
삼풍은 하루에 평균적으로 2천원 손해인 주식이지만, 표준편차가 7만원이나 되기 때문에 기회를 잘 노리면 큰 수익을 얻을 수 있습니다.

actions = c("삼전","네이비","삼풍") # 행동들
mean = c("삼전" = 4000, "네이비" = 3000, "삼풍" = -2000)  # 보상의 모평균(실제 가치)
sd = c("삼전" = 5000, "네이비" = 10000, "삼풍" = 70000)   # 보상의 모표준편차

first_rewards = setNames(c(-4000,1000,100000), actions)  # 보상 = R_1
first_counts = setNames(c(0,0,1), actions)               # 횟수 = 1
first_values = setNames(c(-4000, 1000, 100000), actions) # 가치 = Q_1 (a)
first = list(first_rewards=first_rewards,
             first_counts=first_counts,
             first_values=first_values)

first

mab example

이렇듯, 한 번의 결과로 인해 삼전, 네이비, 삼풍 각각 4천원 손해, 천원 이득, 10만원 이득을 보았고, 삼풍이 선택되었으므로 count가 1 증가했습니다.

이제 그리디 알고리즘으로 어떻게 세 주식 중 수익률이 좋은 주식을 선택하는지 확인해봅시다.

# Greedy
greedy = function(n_iter, actions, first, seed){
  set.seed(seed)
  rewards = first$first_rewards
  counts = first$first_counts
  values = first$first_values
  # 탐욕 알고리즘-------------------------------------------
  for(t in 2:n_iter){
    best = names(which.max(values)) #행동 = A_t 
  
    R = rnorm (1, mean = mean[best], sd = sd[best]) #R_t
    rewards[best] = rewards[best] + R
    
    counts[best] = counts[best] + 1
    values[best] = rewards[best] / counts[best] # 가치 계산
    
    if (t%%10==0) {
      cat(paste0(t,"번째"))
      print(counts)
    t = t+1
    }
  }
  return(list(counts = counts, rewards = rewards, values = values))
}

greedy(100, actions,first,seed=5)

mab greedy

다음과 같이 100일 간 그리디 알고리즘을 적용하여 주식을 선택한다면, 삼풍을 16번까지 선택하고 나서야 손절하고, 삼전으로 갈아타는 것을 볼 수 있습니다. 결과적으로 보상 (rewards)의 총합은 삼전은 약 36만 원, 네이비는 -2.4만 원, 삼풍은 -8.2만 원이 되어 총 수익은 25만 4천 원을 벌었습니다. 일 평균 순이익 (= 기대 순이익) (values)은 삼전은 약 4,500원, 네이비는 - 8,000원, 삼풍은 -5,200원이 됩니다.

직관적으로 아, 이렇게 주식을 선택하면 안 되겠구나 싶죠. 이렇듯 그리디 알고리즘은 탐색을 충분히 하지 않고 활용하기 때문에 좋은 알고리즘이 아닙니다.

입실론-그리디 (Epsilon-Greedy) 알고리즘

10일 중 7일은 기대 수익이 가장 좋은 주식을 선택하고, 3일은 랜덤하게 선택!

입실론-그리디 알고리즘은 그리디 알고리즘에서 탐색을 촉진하기 위해 보완된 알고리즘입니다. 여기서 입실론 ( $epsilon$ )은 작은 수치를 나타내는 그리스 문자로, 무작위로 탐색활 확률을 의미합니다. 즉

$1-\epsilon$ 의 확률로는 그리디 알고리즘 ( $A_t = argmax_a Q_t(a)$ )
$\epsilon$ 의 확률로 랜덤하게 선택

이를 R로 구현하면 다음과 같습니다.

# Epsilon-Greedy
eGreedy = function(n_iter, actions,first, eps = .3, seed){

  set.seed(seed)
  rewards = first$first_rewards
  counts = first$first_counts
  values = first$first_values

  for(t in 2:n_iter){
  
    best = ifelse(eps< runif(1), names(which.max(values)), sample(actions, 1))    
    
    # 보상 업데이트    
    R = rnorm (1, mean = mean[best], sd = sd[best]) #R_t
    rewards[best] = rewards[best] + R
    
    counts[best] = counts[best] + 1 # 횟수
    values[best] = rewards[best] / counts[best] # 가치 계산
    if (t%%10==0) {
      cat(paste0(t,"번째"))
      print(counts)
    }
    t = t+1
  }
  return(list(counts = counts, rewards = rewards, values = values))
}
eGreedy(100, actions, first,seed=5)

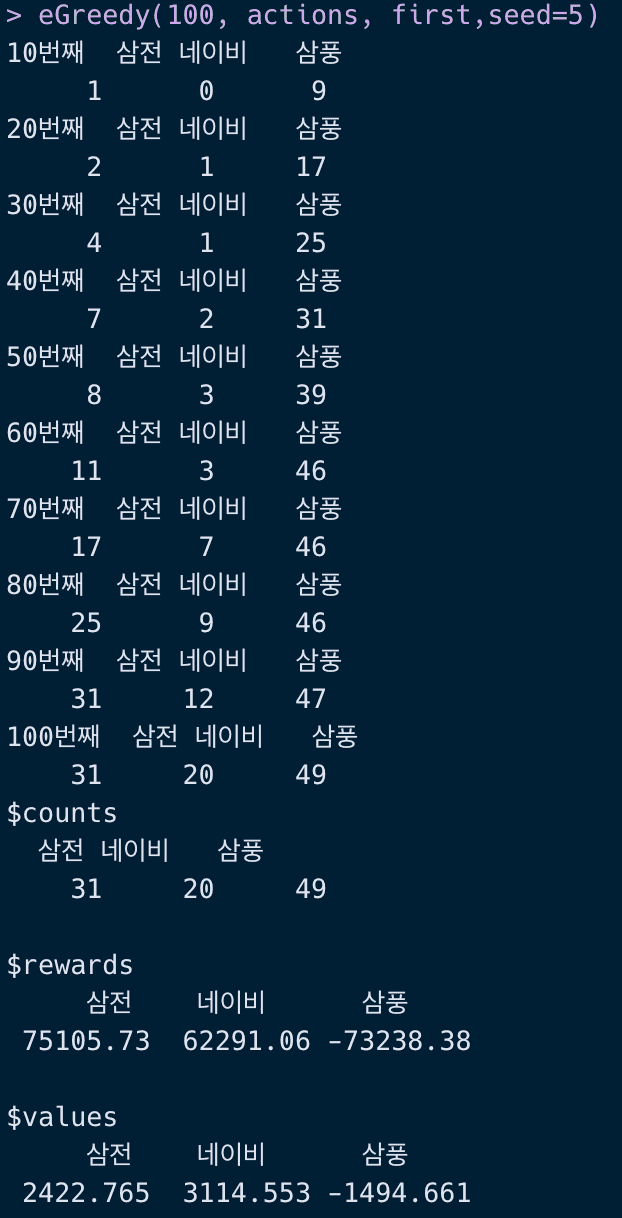
mab egreedy

입실론-그리디 알고리즘을 사용하게 되면 삼풍 주식을 49번이나 구매하게 되네요. 생각보다 야수의 심장입니다. 결과적으로 얻는 수익은 6.4만 원 정도로 그리디 알고리즘을 사용할 때보다 낮습니다.

그 이유는 $\epsilon$ 의 확률만큼 항상 무작위 탐색 (Exploration)을 해야 하기 때문에, 최적의 주식을 찾았더라도 시간이 지나면 최적 값과 멀어지는 결과를 초래할 수도 있기 때문입니다.

UCB (Upper-Confidence-Bound) 알고리즘

탐색과 활용을 적절하게 짬뽕!

입실론-그리디 알고리즘은 최적의 주식을 찾기 위해 랜덤하게 탐험합니다. 그러나 이 랜덤성으로 인해서 최적값과는 멀어지기도 하고 탐색을 과도하게 하는 문제가 있습니다. 예를 들어, 10개의 행동 중 2개가 최선의 산황이여도 입실론-그리디 알고리즘은 나머지 8개도 공평하게 탐색하기 때문에 과도하게 탐색하는 문제가 발생합니다.

이를 해결하기 위해 널리 쓰이는 방법 중 하나는 UCB (Upper-Confidence-Bound) 알고리즘입니다. 이 알고리즘의 아이디어는 추정된 가치 $Q_t(a)$ 에서 일종의 신뢰 구간을 구해서 그 구간의 위쪽 신뢰 구간의 행동을 선택하는 것입니다. 수식으로 쓰면 다음과 같습니다.

A_t = argmax_a [ Q_t(a) + c\sqrt{\frac{\ln t}{N_t(a)}}]

$t$ 는 현재 시점, $N_t(a)$ 는 현재 시점까지 행동 $a$ 를 한 횟수입니다. (R 코드에서 count에 해당) 위 식의 형태를 보면 일반적으로 신뢰구간을 구하는 식 $\mu + c\sqrt{\sigma^2 / n}$ 에서 $\mu$ 대신 $Q_t(a)$ , $\sigma^2$ 대신 $\ln t$ 를 사용한 것만 다름을 알 수 있습니다.

여기서 상수 $c$ 는 신뢰구간 폭을 제어하는 파라미터로, $c$ 를 크게 하면 탐색을 많이 하게 되고 작게 하면 활용을 많이 하게 됩니다. 입실론-그리디 알고리즘에서 입실론이 크면 랜덤하게 탐색할 확률이 커지듯이 $c$ 도 값이 클수록 탐색을 많이 하게 됩니다.

또한 UCB에 들어가는 $c\sqrt{\frac{\ln t}{N_t(a)}}$ 항을 보면, $N_t(a)$ 를 분모에 두어 충분히 탐험되지 않은 행동에 가중치를 줍니다. $N_t(a)$ 가 작을수록 $c\sqrt{\frac{\ln t}{N_t(a)}}$ )은 커지기 때문이죠! 결국 UCB 알고리즘에 들어가는 첫 번째 항 $Q_t(a)$ 은 활용 (Exploitation)에 중점을 둔 항이고, 두 번째 항 $c\sqrt{\frac{\ln t}{N_t(a)}}$ 은 탐색 (Explotation)에 중점을 둔 항이기 때문에 UCB 알고리즘은 활용과 탐색을 적절히 고려해서 선택하는 알고리즘이라 할 수 있습니다.

이를 R로 구현하면 다음과 같습니다.

UCB = function (n_iter, actions, first, control=2,seed){

  set.seed(seed)
  rewards = first$first_rewards
  counts = first$first_counts
  values = first$first_values
  
for(t in 2:n_iter){
  
  # UCB 알고리즘으로 행동을 선택한다
  best = names(which.max(values + control * sqrt(log(t) / counts)))  
  # 보상 업데이트    
  R = rnorm (1, mean = mean[best], sd = sd[best]) #R_t
  rewards[best] = rewards[best] + R
  
  counts[best] = counts[best] + 1
  values[best] = rewards[best] / counts[best] # 가치 계산
  
  if (t%%10==0) {
    cat(paste0(t,"번째"))
    print(counts)
  }
  t = t+1
  }
  return(list(counts = counts, rewards = rewards, values = values))
}
UCB(100, actions,first,seed=5)

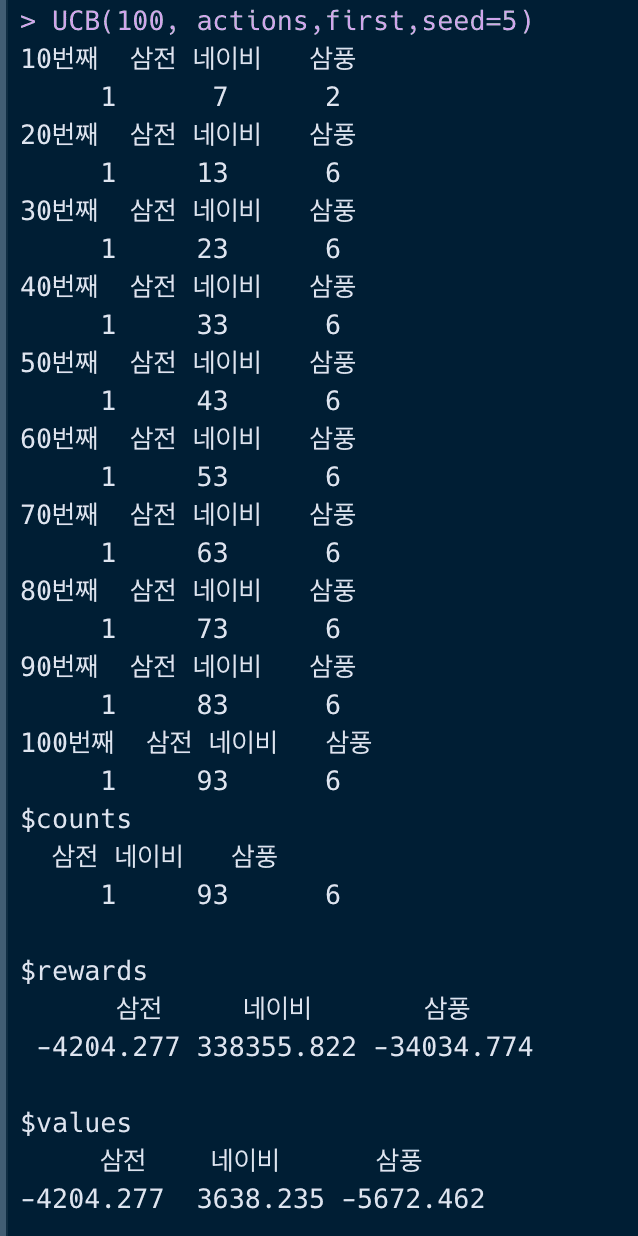
mab ucb

이 때의 결과로 약 30만 원의 이득을 보았네요! 가슴이 웅장해집니다. 그리디 알고리즘과 입실론-그리디 알고리즘과 달리 네이비를 93번이나 택했습니다.

톰슨 샘플링 (Thompson Sampling)

보상에 분포가 있는게 죄는 아니잖아!

톰슨 샘플링은 베이지안 방법으로, 위에서 봤던 알고리즘과는 약간 성격이 다릅니다. 베이지안 방식이기 때문에 관심 있는 모수(에 대해 사전 분포를 정의하고, 관측된 값으로부터 사후 분포를 이끌어냅니다.

톰슨 샘플링을 수도 코드 (pseudo code)를 보면 다음과 같습니다.

mab thompson

여기서

$D$ 는 관측된 값
$\theta^t$ 는 관련 있는 모수들
$x_t$ 는 당시의 상황 (행동별로 얼마나 선택되었는지에 대한 상황)
$r_t$ 은 보상
$a_t$ 는 $t$ 번째 선택된 행동

을 의미합니다. 여기서 $\theta_t$ 는 쉽게 얘기하면 앞서 말씀드린 삼전, 네이비, 삼풍 주식 수익에 대한 모평균과 모표준편차에 해당합니다. 실제 모평균과 모표준편차는 하나의 값으로 정해졌지만, 베이지안은 모평균과 모 표준편차가 하나의 분포 (=사전 분포)를 따른다고 가정하고 이를 데이터 (= 가능도)에 따라 모평균과 모표준편차에 대한 분포를 업데이트 (=사후 분포)하는 방식입니다.

말이 어려운데요. 이에 대한 예를 들자면, 만약 어떤 꼬마가 굉장히 낙천적인 아이여서 엄마가 아이스크림을 사주는 확률을 10번 중 9번 정도 꼴이라 생각하고 있다 가정합시다. 이를 분포로 생각하면 평균 0.9를 갖는 베타 분포입니다. (보통 확률에 대한 사전분포로 베타 분포를 고려하는데, 이는 베타 분포의 값이 항상 0과 1 사이에 있기 떄문입니다)

근데 엄마가 한 달 동안 단 한번도 꼬마에게 아이스크림을 안 사줬다고 가정했을 때, 꼬마는 계속해서 아이스크림을 사줄 확률을 0.9라고 인지하고 있을까요? 아마도 꼬마는 “엄마가 내가 충치가 생겼으니 아이스크림을 덜 사줄꺼야”라 생각하면서 확률을 0.2로 하향 조정할지도 모릅니다. 이렇게 엄마가 한 달 동안 한번도 아이스크림을 사주지 않았다는 것은 30일 간 관측된 값을 의미하고, 이를 함수로 표현하면 가능도 함수 (Likelihood function)이 됩니다. 이 가능도 함수는 이항 분포를 따릅니다. 마지막으로 아이가 확률을 하향조정한 것은 데이터를 관측한 후에 사전 분포를 업데이트하여 사후 분포를 만든 것과 같습니다. 업데이트된 사후 분포는 평균 0.2를 갖는 베타 분포가 되겠네요.

결과적으로 톰슨이라는 분은 이런 베이지안 원리를 MAB에 적용했다 볼 수 있습니다. 저희 주식의 상황으로 보면, 삼전, 네이비, 삼풍의 모평균과 모표준편차에 각각 적당한 분포를 가정하고 (= 사전 분포) 데이터를 받아 모평균과 모표준편차에 대해 업데이트 (=사후 분포)합니다. 이후에 기대 보상 (= 가치)을 최대화하는 행동을 선택하는데요.

제대로 하려면 모평균에 정규 분포, 모표준편차에 위샤트 분포를 가정해서 하는 것이 맞을 것 같으나, 이는 너무 복잡하기 떄문에 단순히 아이스크림 예시처럼 사전 분포를 베타분포로 가정합니다.

사전 분포에 아무런 정보를 두지 않기 위해서 $Beta(1,1)$ 을 가정하고, (= 이는 $Uniform (0,1)$ 와 같으므로 0과 1 사이의 랜덤한 값을 뽑는 것과 같습니다.)
가능도를 $x \sim Bernoulli(p_a)$ 로 두면,
사후 분포를 $Beta(x+1,n-x+1)$ 로 업데이트할 수 있습니다.

이제 이를 R로 구현하면 다음과 같습니다.

Thompson = function(n_iter,actions,first,probs, seed){
  
  set.seed(seed)
  n_actions = length(actions)
  rewards = ifelse (first$first_rewards>0, 1,0) # 보상을 받으면 1, 못받으면 0
  counts = first$first_counts
  values = first$first_values

  for (t in 2:n_iter) {
    B<-matrix(rbeta(n_actions, rewards+1, (counts-rewards)+1),1, byrow = TRUE)
    P<-table(factor(max.col(B), levels=1:ncol(B)))/nrow(B)
    # tmp are the weights for each time step
    tmp<-round(P*1,0)
    
    # Update the Rewards
    rewards = rewards+rbinom(rep(1,n_actions), size=P, prob = probs)
    
    #Update counts
    counts = counts+tmp
    
  }
  return(setNames(counts, actions))
}

set.seed(5)
probs<-c(sum(rnorm(1000, mean['삼전'], sd['삼전'])>0) / 1000,
         sum(rnorm(1000, mean['네이비'], sd['네이비'])>0) / 1000,
         sum(rnorm(1000, mean['삼풍'], sd['삼풍'])>0) / 1000)

probs= setNames(probs,actions)
probs
Thompson(100, actions,first, probs, seed=5)

mab thompson2

여기서 삼전, 네이비, 삼풍 주식을 통해 보상을 얻을 확률을 위에서 세운 모평균과 모표준편차로 각각 1,000번 정규분포 난수를 뽑아서 0보다 클 확률로 두어 계산했습니다. 그 때의 확률값은 각각 삼전 = 0.798, 네이비 = 0.652, 삼풍 = 0.478입니다. 이 확률로 톰슨 샘플링을 하게 되면 다음과 같이 삼전 80번, 네이비 12번, 삼풍 8번의 결과를 얻게 됩니다.

마무리

각 알고리즘마다 주요하게 사는 주식이 다른게 흥미로운 것 같습니다. 개인적으로 톰슨 샘플링으로 그래서 얼마나 수익률을 가져왔는지 보여주지 못하는건 아쉬운데요. 그래서 다음번에는 실제 주식 데이터로 어떤 주식을 구매하면 좋을지 톰슨 샘플링을 이용한 MAB를 적용해보도록 하겠습니다. (아마도 ㅠㅠ)

Table Of Contents

A/B 테스트는 항상 어렵다

MAB가 왜 똑똑한가

MAB에 쓰이는 용어

MAB에 쓰이는 네 개의 알고리즘

그리디 (Greedy) 알고리즘

입실론-그리디 (Epsilon-Greedy) 알고리즘

UCB (Upper-Confidence-Bound) 알고리즘

톰슨 샘플링 (Thompson Sampling)

마무리

References

Tags

Share

Related Posts

Table Of Contents

.css-1qh5hbx{box-sizing:border-box;margin:0;min-width:0;display:block;color:var(--theme-ui-colors-heading,#2d3748);font-weight:bold;-webkit-text-decoration:none;text-decoration:none;margin-bottom:1rem;font-size:1.5rem;position:relative;}A/B 테스트는 항상 어렵다

.css-c6w1gk{box-sizing:border-box;margin:0;min-width:0;display:block;color:var(--theme-ui-colors-heading,#2d3748);font-weight:bold;-webkit-text-decoration:none;text-decoration:none;margin-bottom:1rem;font-size:1.25rem;position:relative;}MAB에 쓰이는 용어

Tags

Share

Related Posts

A/B 테스트는 항상 어렵다

MAB에 쓰이는 용어