Table Of Contents
- 이번 포스팅은 지난 LTV (Life Time Value) 지표 속 BG/NBD 모델과 Gamma-Gamma 모델 파헤치기에 이어 실제 데이터를 통해 LTV를 계산해보는 포스팅입니다.
- 참조한 데이터는 UCI Machine Learning Repository 의 Online Retail Dataset이며, databricks LTV 분석 자료를 주로 참조하였습니다.
- 전체 코드는 이 곳에서 확인하실 수 있습니다.
- 원 글은 이 곳에서 확인하실 수 있습니다.
세 줄 요약
본격적으로 데이터 분석을 하기 전에 LTV가 무엇이고 어떻게 계산하는지 세 줄로 말씀드리겠습니다.
- LTV는 고객이 평생동안 기업에게 어느 정도의 금전적 가치를 가져다 주는지를 정량화한 지표로, 고객별 미래의 예상 구매 횟수 * 예상 평균 수익으로 계산됩니다.
- 미래의 예상 구매 횟수는 BG/NBD 모형을 통해 산출되며, 이를 위해 R (Recency), F (Frequency), T (Time) 정보가 필요합니다.
- 미래의 예상 평균 수익은 Gamma-Gamma 모형을 통해 산출되며, 이를 위해 F (Frequency), M (Monetary Value) 정보가 필요합니다.
그래서 저희는 구매 기록 데이터의 R, F, M, T를 구해 BG/NBD 모형과 Gamma-Gamma 모형을 각각 적합해 LTV를 구할 것입니다. 구체적인 R, F, M, T는 이전 포스팅을 참조해주셔도 되고, 이번 포스팅에서도 예시로 구해볼 예정이니 걱정 마세요~!
Online Retail 데이터 살펴보기
먼저 저희가 LTV를 계산할 때 필요한 모듈은 다음과 같습니다.
여기서 lifetimes 모듈이 바로 LTV를 구할 때 필요한 모듈이니 기억해주세요!
import pandas as pdimport warningsimport osimport numpy as npimport matplotlib.pyplot as pltfrom datetime import datetimefrom datetime import timedeltafrom lifetimes.plotting import *from lifetimes.utils import *from lifetimes import BetaGeoFitterfrom lifetimes.fitters.gamma_gamma_fitter import GammaGammaFitterfrom hyperopt import hp, fmin, tpe, rand, SparkTrials, STATUS_OK, space_eval, Trialswarnings.filterwarnings('ignore')os.chdir('/Users/eunji/Library/Mobile Documents/com~apple~CloudDocs/data-analysis/LTV/')
데이터를 불러오면 아래와 같은 형태를 띠고 있습니다.
df = pd.read_excel("Online Retail.xlsx")df.head()

각 컬럼에 대한 설명은 다음과 같습니다.
- InvoiceNo: 송장 번호
- StockCode: 제품 번호
- Description: 제품명
- Quantity: 주문 수량
- InvoiceDate: 주문 일자 및 시각 (datetime 형태)
- UnitPrice: 단가 (화폐 단위: 파운드 £)
- CustomerID: 고객 번호
- Country: 고객 거주 국가
데이터 전처리
여기서 저희가 필요한 정보는 고객마다 일자별로 얼마치를 구매했는지인데요. 이를 위해 전처리를 해줍니다.
# InvoiceDate (주문 일자): Datetime -> date형df['InvoiceDate'] = pd.to_datetime(df['InvoiceDate']).dt.date# CustomerID: NULL인 것 제외df = df[pd.notnull(df['CustomerID'])]# Quantity (주문 수량): 1 이상인 것df = df[(df['Quantity'] > 0)]# Sales (구매 금액) 변수 생성df['Sales'] = df['Quantity'] * df['UnitPrice']# 고객 번호, 주문 일자, 구매 금액만 남기고 지우기cols_of_interest = ['CustomerID', 'InvoiceDate', 'Sales']df = df[cols_of_interest]
주석에 써있는 것처럼 아래와 같은 전처리를 하였습니다.
- InvoiceDate: Datetime -> date형으로 변환
- CustomerID: NULL인 것 제외
- Quantity: 1 이상인 것만 가져오기
- Sales 변수 생성
- 고객 번호, 주문 일자, 구매 금액만 남기고 지우기
그렇게 전처리를 하면 이렇게 CustomerID (고객 번호), InvoiceDate (주문 일자), Sales (구매 금액) 컬럼을 가진 고객별 일자별 구매기록 데이터가 남게 됩니다.
df.head()
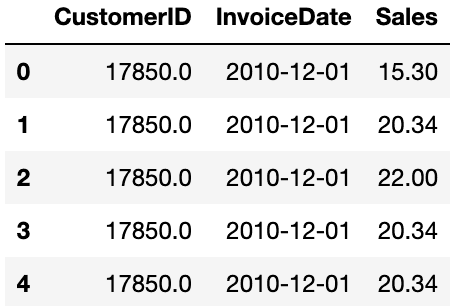
그림에서 볼 수 있듯이 한 고객이 하루에 여러 번 구매했을 경우 굳이 일자별로 구매 금액을 합해 한 행으로 남길 필요는 없고, 그대로 두어도 괜찮습니다.
lifetimes 패키지로 RFMT 계산하기
lifetimes.utils 모듈의
summary_data_from_transaction_data함수
이제 다음에 할 일은 BG/NBD 모형과 Gamma-Gamma 모형의 INPUT이 되는 R, F, M, T를 만드는 일입니다.
이는 lifetimes의 summary_data_from_transaction_data 함수를 이용해 쉽게 만들 수 있습니다.
current_date = df['InvoiceDate'].max()metrics_df = summary_data_from_transaction_data(df, customer_id_col = 'CustomerID', datetime_col = 'InvoiceDate', monetary_value_col='Sales', observation_period_end=current_date)metrics_df.head()
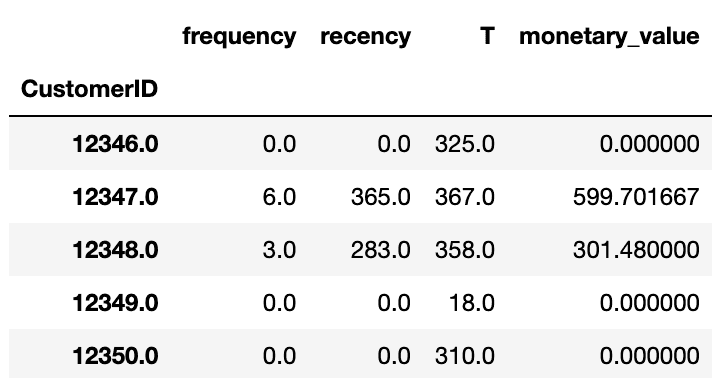
summary_data_from_transaction_data는 raw 형태의 구매 기록 데이터에서 고객별 R, F, M, T를 계산해주는 함수입니다.
그림에서 각 컬럼에 대한 설명은 다음과 같습니다.
| 컬럼명 | 변수 | 설명 |
|---|---|---|
| frequency | F | 고객별 구매 일수 |
| recency | R | 고객별 첫 구매 ~ 마지막 구매까지의 시간 |
| T | T | 고객별 첫 구매 ~ 집계일까지의 시간 |
| monetary_value | M | 고객별 평균 구매 금액 |
RFMT 손계산하기
RFMT가 구체적으로 어떻게 계산되는지 확인하기 위해 한 고객의 RFMT를 구해봅시다.
CustomerID = 12347인 고객의 RFMT는 다음과 같습니다.
# 예시metrics_df[metrics_df.index==12347]

즉,
- 총 6번 구매했고 (frequency),
- 마지막 구매일 - 첫 구매일은 365일 (recency),
- 집계일 - 첫 구매일은 367일 (T)이며,
- 평균 구매 금액은 £600 정도 (monetary_value)임을 의미합니다.
이를 손계산해보겠습니다. 먼저 CustomerID = 12347인 유저 데이터는 아래와 같습니다.
## 수동 계산해보기!example = df[df['CustomerID']==12347]example.head()
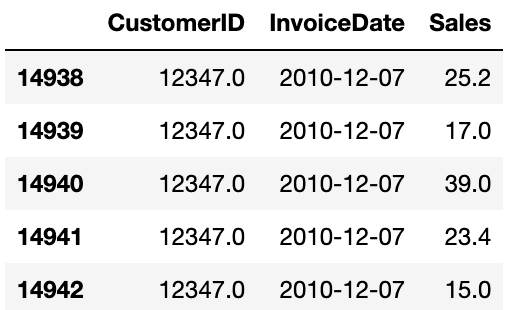
이 고객의 RFMT를 구하면 다음과 같습니다.
# frequency = 6, 구매 일수print(len(example['InvoiceDate'].unique())-1)# recency = 365: 최대 주문일 - 최소 주문일print(max(example['InvoiceDate']) - min(example['InvoiceDate']))# T = 367: 집계일 - 최소 주문일print(current_date - min(example['InvoiceDate']))# monetary_value = 599.701667, 평균 구매 금액ex_daily_sales = example.groupby("InvoiceDate")["Sales"].sum()print(np.mean(ex_daily_sales[1:]))
6365 days, 0:00:00367 days, 0:00:00599.7016666666667
- frequency (F)는
InvoiceDate의 유니크 개수 - 1 (첫 구매일은 포함하지 않습니다) - recency (R)은
CustomerID= 12347 고객의InvoiceDate최대값 - 최소값 - time (T)은 집계일
current_date에서InvoiceDate최소값 - monetary_value (M)는 일별 구매 금액의 평균 (마찬가지로 첫 구매일은 포함하지 않습니다) 로 계산됩니다.
F와 M을 계산할 때 첫 구매일을 제외하는 이유는 “반복되는 구매 행위”에 대한 통계를 계산하고 있기 때문에 시작점을 포함하지 않습니다.
최적의 L2 penalty 파라미터 찾기
이제 고객 각각의 RFMT를 계산했으니 이 데이터를 BG/NBD 모형과 Gamma-Gamma 모형의 INPUT으로 넣어주면 됩니다.
그런데 모형을 적합시킬 때 다음과 같이 penalizer_coef 인자에 L2 penalty를 넣어준다면 모형을 좀 더 강건하게 만들어줄 수 있습니다.
model = BetaGeoFitter(penalizer_coef=l2_reg)model = GammaGammaFitter(penalizer_coef=l2_reg)
lifetimes 공식 홈페이지에서는 데이터 크기가 작으면 추정된 파라미터들이 과도하게 추정될 수 있어서 가능도에 L2 penalty를 부여할 수 있다고 말합니다. 이 L2 penalty는 0.001 ~ 0.1 사이로 넣어야 효과적이라 하네요! L2 penalty에 대한 원론적인 설명은 Ridge/Lasso Regression 포스팅을 참조해주세요!
어쨌든 다시 본론으로 돌아와서 L2 penalty의 계수를 어떻게 넣어줘야 최적인지 파라미터를 찾는 과정이 필요합니다.
이를 위해 databricks LTV 분석 자료에선 hyperopt 모듈을 이용해 베이지안 하이퍼파라미터 튜닝을 진행하였습니다.
훈련 / 테스트 데이터 나누기
lifetimes.utils 모듈의
calibration_and_holdout_data함수
어떤 L2 penalty가 “최적”인지 알려면 적당하게 데이터를 나눠 훈련시키고 테스트하는 과정이 필요하겠죠? lifetimes 패키지에서는 훈련 데이터를 calibration data / 테스트 데이터를 holdout data라 부릅니다.
굳이 train / test 데이터라 부르지 않는 이유는 train/test 데이터는 랜덤하게 일정 비율로 나눈다면, 시계열 데이터는 랜덤하게 나누지 않고 특정 시점의 전과 후로 나누기 때문에 용어를 따로 쓰는 게 아닌가 생각이 들었습니다.
그럼 어느 시점을 전후로 calibration과 holdout으로 나눌 것이냐? 에 대해선 정해진게 없네요. databricks LTV 분석 자료 에서는 마지막 90일 동안을 holdout data로 두고 있고 어디선 2:1로 나눴다는 것도 봤습니다.
우선 저희는 데이터 크기가 거의 1년이기 때문에 마지막 세 달 (90일)을 기준으로 데이터를 나눠보겠습니다.
calibration_and_holdout_data 인자는 아까 summary_data_from_transaction_data와 거의 비슷한데 calibration_period_end만 추가되었습니다.
이 인자에는 calibration data가 끝나는 시점 (90일 이전 날짜)인 calibration_end_date로 적어주면 됩니다.
holdout_days = 90calibration_end_date = current_date - timedelta(days = holdout_days)metrics_cal_df = calibration_and_holdout_data(df,customer_id_col = 'CustomerID',datetime_col = 'InvoiceDate',calibration_period_end=calibration_end_date # train 데이터 기간,observation_period_end=current_date # 끝 기간,monetary_value_col='Sales')metrics_cal_df.head()
또한 summary_data_from_transaction_data 결과와 달리 RFMT에 _cal과 _holdout이 붙었는데요.
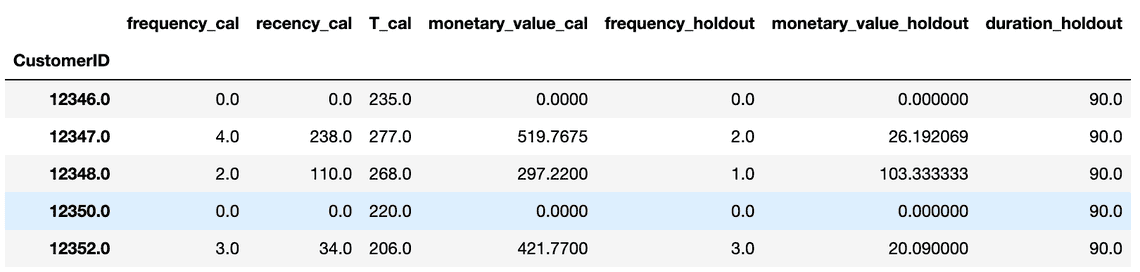
- calibration 기간 동안의 RFMT를 계산한 값은
_cal이 붙고, holdout 기간 동안의 F와 M을 계산한 값은_holdout이 붙습니다. duration_holdout은 holdout data이 며칠인지 나타내는 컬럼입니다.
최종 데이터 만들기
고객별 RFMT가 들어간 데이터에서 frequency가 1 이상인 데이터만 가져오기!
이렇게 하면 BG/NBD 모형과 Gamma-Gamma 모형의 INPUT을 정리할 수 있습니다.
아래 코드에서 보면 frequency가 0인 것은 제외하고 가져오는데, 이 고객들은 전체 기간 동안 구매 일수가 1일인 유저입니다. (frequency는 총 구매일수 - 1) 이들은 “반복적인” 구매를 한 고객들이 아니라서 BG/NBD 모형 가정에서 벗어난 고객들이기 때문에 제외하고 적합해야 합니다.
## frequency가 0인 것은 제외하기whole_filtered_df = metrics_df[metrics_df.frequency > 0]filtered_df = metrics_cal_df[metrics_cal_df.frequency_cal > 0]
whole_filtered_df는 L2 페널티를 최적화한 후에 제일 마지막에 LTV를 계산할 때 쓸 데이터이고 (calibration / holdout을 나누지 않은 데이터)filtered_df는 L2 페널티를 최적화하기 위해 calibration / holdout을 나눈 데이터입니다.
L2 페널티 최적화하기
hyperopt 모듈의
fmin함수
자, 이제 훈련과 테스트 데이터를 나눴으니 L2 페널티를 최적화할 차례입니다. 이를 위해 세 가지 함수를 정의합니다.
score_model: 실제값과 예측값의 차이에 대한 지표 (MSE / RMSE/ MAE)를 계산하는 함수evaluate_bgnbd_model: calibration data와 l2_reg를 넣어 BG/NBD 모형을 적합시키고, holdout data의 구매 일수 (frequency)에 대한 실제값과 예측값에 대한 MSE를 계산하는 함수evaluate_gg_model: calibration data와 l2_reg를 넣어 Gamma-Gamma 모형을 적합시키고, holdout data의 평균 구매 금액 (monetary value)에 대한 실제값과 예측값에 대한 MSE를 계산하는 함수
# 평가 지표: default는 MSEdef score_model(actuals, predicted, metric='mse'):metric = metric.lower()# MSE / RMSEif metric=='mse' or metric=='rmse':val = np.sum(np.square(actuals-predicted))/actuals.shape[0]elif metric=='rmse':val = np.sqrt(val)# MAEelif metric=='mae':val = np.sum(np.abs(actuals-predicted))/actuals.shape[0]else:val = Nonereturn val# BG/NBD 모형 평가def evaluate_bgnbd_model(param):data = inputsl2_reg = param# 모형 적합model = BetaGeoFitter(penalizer_coef=l2_reg)model.fit(data['frequency_cal'], data['recency_cal'], data['T_cal'])# 모형 평가frequency_actual = data['frequency_holdout']frequency_predicted = model.predict(data['duration_holdout'], data['frequency_cal'], data['recency_cal'], data['T_cal'])mse = score_model(frequency_actual, frequency_predicted, 'mse')return {'loss': mse, 'status': STATUS_OK}# Gamma/Gamma 모델 평가def evaluate_gg_model(param):data = inputsl2_reg = param# GammaGamma 모형 적합model = GammaGammaFitter(penalizer_coef=l2_reg)model.fit(data['frequency_cal'], data['monetary_value_cal'])# 모형 평가monetary_actual = data['monetary_value_holdout']monetary_predicted = model.conditional_expected_average_profit(data['frequency_holdout'], data['monetary_value_holdout'])mse = score_model(monetary_actual, monetary_predicted, 'mse')# return score and statusreturn {'loss': mse, 'status': STATUS_OK}
이 후 hyperopt 모듈의 fmin 함수를 이용해 BG/NBD 모형과 Gamma-Gamma 모형 각각의 최적의 L2 penalty를 찾습니다.
- BG/NBD의
penalizer_coef= 0.9993016562948857
search_space = hp.uniform('l2', 0.0, 1.0)algo = tpe.suggesttrials = Trials()inputs = filtered_dfargmin = fmin(fn = evaluate_bgnbd_model, # 목적함수space = search_space, # 파라미터 공간algo = algo, # 최적화 알고리즘: Tree of Parzen Estimators (TPE)max_evals=100, # 반복수trials=trials)l2_bgnbd = space_eval(search_space,argmin)print(l2_bgnbd)> 0.9993016562948857
- Gamma-Gamma의
penalizer_coef= 0.011236999455395335
trials = Trials()# GammaGammaargmin = fmin(fn = evaluate_gg_model,space = search_space,algo = algo,max_evals=100,trials=trials)l2_gg = space_eval(search_space,argmin)print(l2_gg)> 0.011236999455395335
BG/NBD 모형 및 Gamma-Gamma 모형 적합하기
이제 최적의 L2 penalty를 찾았으니 이를 이용해 BG/NBD 모형과 Gamma-Gamma 모형을 적합할 차례입니다! 최적의 L2 penalty를 넣었을 때 holdout 데이터로 각 모형의 MSE를 구해보겠습니다.
BG/NBD 모형 적합
BetaGeoFitter (penalizer_coef)및predict함수
BG/NBD 모형은 고객별 미래의 구매 횟수를 예측하기 위한 모형입니다. 이를 위해 아래처럼
- 최적의 L2 penalty
l2_bgnbd를 넣고, calibration data로 모형을 적합시킨 후 - holdout data로 frequency의 실제값과 예측값을 비교해 MSE를 계산합니다.
lifetimes_model = BetaGeoFitter(penalizer_coef=l2_bgnbd) #l2_bgnbd = hyperopt로 나온 결과# calibration 데이터의 R,F,T로 모형 적합lifetimes_model.fit(filtered_df['frequency_cal'], filtered_df['recency_cal'], filtered_df['T_cal'])# holdout 데이터로 모델 평가: F의 실제값과 예측값의 MSEfrequency_actual = filtered_df['frequency_holdout']frequency_predicted = lifetimes_model.predict(filtered_df['duration_holdout'],filtered_df['frequency_cal'], filtered_df['recency_cal'], filtered_df['T_cal'])mse = score_model(frequency_actual, frequency_predicted, 'mse')print('MSE: {0}'.format(mse))> MSE: 2.9944204820420146
그 결과 MSE는 2.99 정도네요. 구매 일수에 대한 평균 제곱 오차가 +- 3일 정도 됨을 알 수 있습니다.
또한, 이 lifetimes_model을 통해 BG/NBD 모형에서 추정된 파라미터들을 확인할 수 있습니다.
lifetimes_model.summary
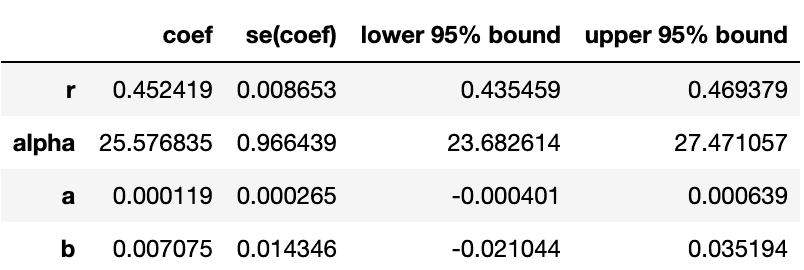
r, alpha, a, b 모수가 나오는데요. 지난 포스팅에서 이 모수들은 고객별 구매율과 이탈률에 대한 모수라 설명한 바가 있습니다.
다시 설명을 하면 BG/NBD 모형은 다음과 같은 가정을 하고 있습니다.
- 고객이 남아있는 동안, 일정한 기간 동안의 구매 횟수는 Pois()를 따릅니다. 위에서 말씀 드렸듯이 1일 간 Pois (1/12)를 따른다면 T= 1년일 경우 Pois (30)을 따르게 되겠죠! (포아송의 모수인 는 예상 구매 횟수 를 의미합니다)
- 고객마다 일정한 기간 동안 구매하는 횟수는 다릅니다. 이는 ~ Gamma (r,)을 따릅니다.
- j번째 구매가 마지막이고 더 이상 구매를 하지 않을 확률 (이탈률)은 입니다. 이탈할 때까지의 구매 횟수는 Geo (p)를 따릅니다.
- 고객마다 더 이상 구매를 하지 않을 확률 (이탈률)은 다릅니다. 이탈률 p는 p ~ Beta (a,b)를 따릅니다.
- 고객별 일정 기간 동안의 구매 횟수와 구매를 하지 않을 확률은 서로 영향을 주지 않습니다.
여기서 2번에 해당하는 Gamma(r, )와 4번에 해당하는 Beta(a, b)가 lifetimes_model에서 추정되는 파라미터인 것입니다.
이를 활용해 고객마다 일정한 기간 동안 구매하는 횟수의 분포와 고객별 더 이상 구매하지 않을 확률�의 분포도 그릴 수 있겠네요!
먼저, 고객마다 일정한 기간 동안 구매하는 횟수 는 Gamma(r,alpha)을 따릅니다.
# 고객별 lambda (구매율) 의 분포from scipy.stats import gammaimport matplotlib.pyplot as pltcoefs = lifetimes_model.summary['coef']x = np.linspace (0, 2, 100)y = gamma.pdf(x, a=coefs['r'], scale=1/coefs['alpha']) # BG/NBD에서의 모수 alpha는 scale 모수가 아닌 rate 모수이므로 역수!plt.plot(x, y)
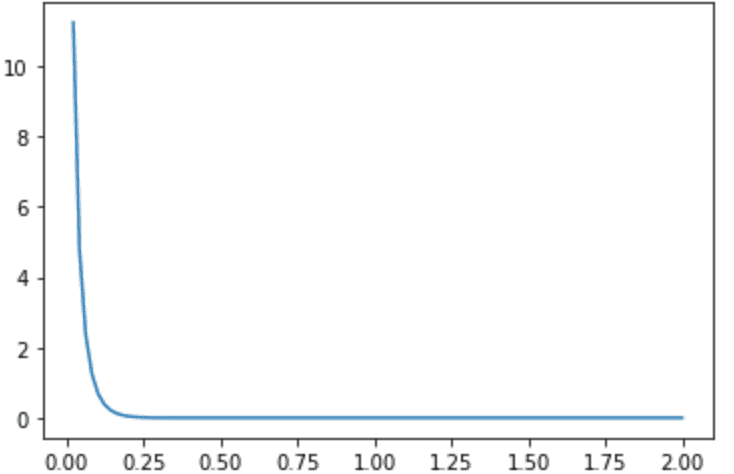
여기서 T 기간동안의 평균 구매 횟수가 이므로 에 대한 분포는 1일 단위입니다.
위 그림에서 0.2쯤부터 확률이 0으로 수렴하고 있는데 대부분 고객들이 1일의 평균 구매 횟수는 최대 0.2 정도임을 의미합니다. 즉, 최대 5일에 한 번 꼴로 구매한다라 볼 수도 있겠죠!
두 번째로, 고객이 더 이상 구매를 하지 않을 확률은 Beta(a,b)를 따릅니다.
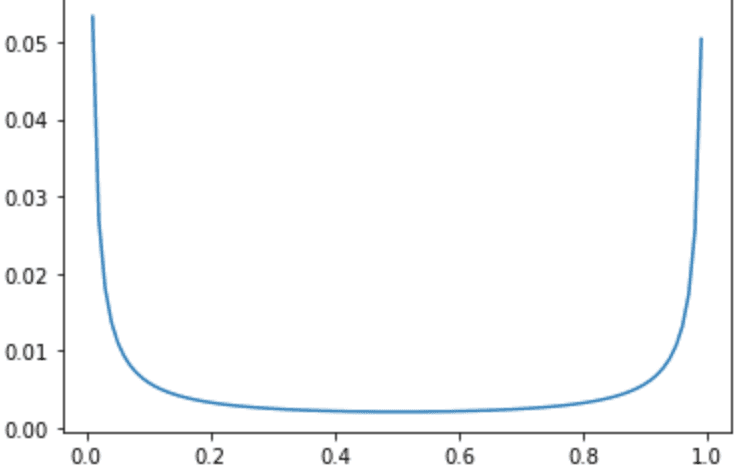
분포가 0과 1 근처로 양극단에 위치한 것을 볼 수 있습니다. 즉 더 이상 구매를 하지 않을 확률이 0인 active한 유저도 많고, 확률이 1 근처인 inactive한 유저도 많음을 알 수 있습니다.
Gamma-Gamma 모형 적합
GammaGammaFitter (penalizer_coef)와conditional_expected_average_profit함수
각설하고 이제 “평균 구매 금액”을 모델링하기 위한 Gamma-Gamma 모형을 적합해봅시다.
이를 위해 BG/NBD 모형때와 마찬가지로
- 최적의 L2 penalty
l2_gg를 넣고, calibration data로 모형을 적합시킨 후 - holdout data로 monetary value의 실제값과 예측값을 비교해 MSE를 계산합니다.
spend_model = GammaGammaFitter(penalizer_coef=l2_gg)spend_model.fit(filtered_df['frequency_cal'], filtered_df['monetary_value_cal'])# conditional_expected_average_profit: 고객별 평균 구매 금액 예측monetary_actual = filtered_df['monetary_value_holdout']monetary_predicted = spend_model.conditional_expected_average_profit(filtered_df['frequency_holdout'],filtered_df['monetary_value_holdout'])mse = score_model(monetary_actual, monetary_predicted, 'mse')print('MSE: {0}'.format(mse))> MSE: 364.3300491426786
평균 구매 금액의 평균 제곱 오차는 £364정도 된다 나옵니다.
히스토그램을 통해 실제와 예측된 평균 구매 금액이 어떻게 차이가 나는지 확인해봅�시다.
bins = 100plt.figure(figsize=(15, 5))plt.hist(monetary_actual, bins, label='actual', histtype='bar', color='STEELBLUE', rwidth=0.99)plt.hist(monetary_predicted, bins, label='predict', histtype='step', color='ORANGE', rwidth=0.99)plt.legend(loc='upper right')
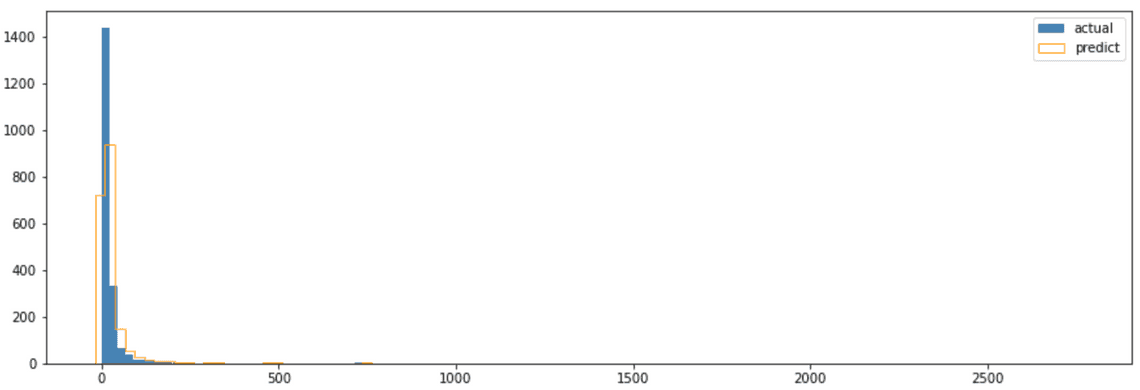
파란 막대가 실제값, 주황 투명 막대가 예측값입니다. 어느 정도 분포가 비슷함을 볼 수 있죠.
만약 penalizer_coef를 주지 않고 예측할 경우 어떨까요?
# penalizer_coef 없이 �했을 때의 결과spend_model = GammaGammaFitter(penalizer_coef=0)spend_model.fit(filtered_df['frequency_cal'], filtered_df['monetary_value_cal'])# 평가monetary_actual = filtered_df['monetary_value_holdout']monetary_predicted = spend_model.conditional_expected_average_profit(filtered_df['frequency_holdout'],filtered_df['monetary_value_holdout'])mse = score_model(monetary_actual, monetary_predicted, 'mse')bins = 100plt.figure(figsize=(15, 5))plt.hist(monetary_actual, bins, label='actual', histtype='bar', color='STEELBLUE', rwidth=0.99)plt.hist( monetary_predicted, bins, label='predict', histtype='step', color='ORANGE', rwidth=0.99)plt.legend(loc='upper right')
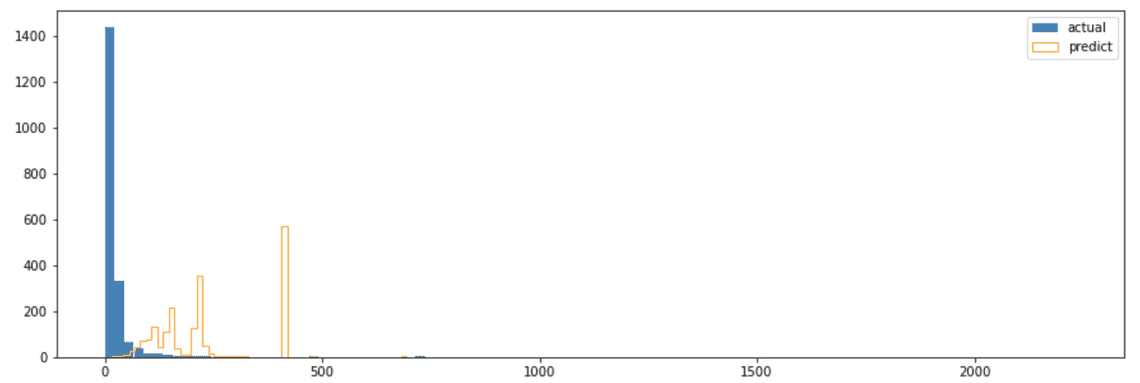
penalized_coef=0으로 두었을 땐 파란 막대와 주황 막대의 분포가 전혀 다름을 확인할 수 있습니다. (예측 꽝!)
LTV 구하기
customer_lifetime_value함수
우여곡절 끝에 이제 LTV를 구할 준비는 끝났습니다. 지금까지는
- 고객별 RFMT를 구하였고
- calibration/holdout 데이터를 나눠 L2 penalty 최적화를 하였고
- 최적화된 값을 BG/NBD 모형에 넣어 예상 구매 일수를
- 최적화된 값을 Gamma-Gamma 모형에 넣어 예상 구매 금액을 구하였습니다.
이제 BG/NBD 모형과 Gamma-Gamma 모형을 합쳐 LTV를 구할 차례입니다.
lifetimes_model은BetaGeoFitter를 통해 나온 모형이고spend_model은GammaGammaFitter를 통해 나온 모형입니다.
이를 통해 아래와 같이 final_df에 ltv 컬럼을 추가할 수 있습니다.
final_df = whole_filtered_df.copy()final_df['ltv'] = spend_model.customer_lifetime_value(lifetimes_model,final_df['frequency'],final_df['recency'],final_df['T'],final_df['monetary_value'],time=12,discount_rate=0.01 # monthly discount rate ~12.7% 연간)
- 여기서 왜
filtered_df대신whole_filtered_df를 쓰냐면, calibration/holdout로 나뉘어진 데이터가 아닌 전체 데이터를 대상으로 LTV를 구해야하기 때문이며 time과discount_rate는 향후 몇 개월동안의 LTV를 볼 것인지 (time = 12개월), 어느 정도의 할인율을 적용할 것인지 (discount_rate=0.01) 정하는 인자입니다. 예를 들어discount_rate=0.01이면 (1.01)^12 = 1.127 = 1+ 0.127 = 12.7% 만큼 ltv가 할인 (감소)하도록 계산해주는 것 같습니다.
또한 BG/NBD 모형의 OUTPUT인 정해진 기간만큼의 예상 구매 횟수도 구할 수 있습니다. 365일 동안의 예상 구매 횟수를 구하려면 다음과 같습니다.
t=365 #365일final_df['predicted_purchases'] = lifetimes_model.conditional_expected_number_of_purchases_up_to_time(t, final_df['frequency'], final_df['recency'], final_df['T'])
마지막으로 Gamma-Gamma 모형의 OUTPUT인 예상 평균 구매 금액은 다음과 같이 구할 수 있습니다.
final_df['predicted_monetary_value'] = spend_model.conditional_expected_average_profit(final_df['frequency'],final_df['monetary_value'])
누가 가장 높은 LTV를 가졌고, 왜 그럴까?
그럼 누가 LTV가 가장 많이 높은지 확인해볼까요?
final_df.sort_values(by="ltv").tail(5)
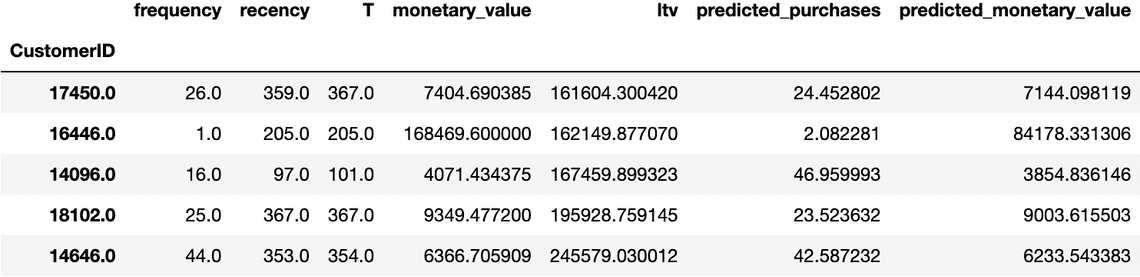
영예의 1위는 CustomerID=14646번 고객으로, LTV가 £245,579 였습니다. 한국 돈으로 환산하니 약 3.9억이 되는 고객이네요 ㄷㄷ. 왜 그렇게 높게 나왔을까요?
- 이 분의 평균 구매 금액 (monetary_value)은 £6,367 정도로 한 번에 1천만 원 쓰시는 분이구요.
- 354일 동안 44번 구매했습니다. (평균 8일에 한 번 꼴)
- 어제도 구매하셨네요. (T-recency = 집계일 - 마지막 구매 일자가 1이므로)
LTV 모형을 고려하지 않고 계산하면 다음 해에도 1천만 원씩 * 44번 = 4.4억 정도 구매할 거라 예상하겠죠?
그러나 BG/NBD 모형과 Gamma-Gamma 모형을 통해 나온 LTV는 3.9억으로 5천만 원 정도 더 적게 예측했습니다.
- 우선 BG/NBD 모형을 통해 나온 예상 구매 횟수 (predicted_purchases)는 43번 정도이고
- Gamma-Gamma 모형을 통해 나온 평균 구매 금액 (predicted_monetary_value)는 £6,234 정도입니다.
- 이 둘을 곱한 금액은 £268,092 정도이죠.
- 여기서 discount_rate까지 고려하여 최종적으로 £245,579 정도로 나왔습니다.
이처럼 과거의 구매 기록 데이터를 바탕으로 어느 정도 감소된 (=더 타당한) 값을 도출해냈습니다.
마치며
python의 lifetimes 패키지를 이용해 고객의 구매 기록 데이터를 통해 LTV를 계산해보았습니다.
개인적으로 lifetimes 함수명이 너무 길어서 이해하기 좀 어렵고, 가이드 문서도 많지 않아 적용하는데 어려움을 겪었었는데요.
이 글을 읽으신 분들은 그나마 한글로 된 LTV 자료를 겟또하시는 바람으로, 그리고 저도 정리된 문서를 가질 목적으로 글을 정리했습니다.
함수들의 쓰임을 요약하며 이 글을 마칩니다!
| 함수명 | 용도 |
|---|---|
| summary_data_from_transaction_data | 구매기록 데이터에서 고객별 RFMT 계산 |
| calibration_and_holdout_data | 훈련 / 테스트를 나눠 고객별 RFMT 계산 |
| fmin | L2 penalty 최적화 |
| BetaGeoFitter | 예상 구매 일수를 구하기 위한 BG/NBD 모형 적함 |
| conditional_expected_number_of_purchases_up_to_time | t 시점까지의 예상 구매 일수 계산 |
| GammaGammaFitter | 예상 평균 구매 금액을 구하기 위한 Gamma-Gamma 모형 적합 |
| conditional_expected_average_profit | 예상 평균 구매 금액 계산 |
| customer_lifetime_value | ��고객별 LTV 계산 |
