Table Of Contents
🙆🏻♂️ 본 글은 개인블로그에서도 확인 가능합니다.
과거 다른 글에서 아래와 같은 얘기를 한 적이 있습니다.
회사는 매일, 매주, 매월, 매년 새로운 의사결정을 내리고 새로운 실행을 합니다. 회사상황에 맞게 적정수준의 인과추론 포맷을 만들고 회사 의사결정 사이클에 맞춰 빠르게 분석 결과를 내도록 인과분석이 성숙해져야 탁상공론이 아닌 인과분석이 자리 잡을 수 있을 것 같습니다.
위 내용처럼 연구원이 아닌 회사원으로서 인과분석을 잘 사용하기 위해서는 상황별 적절한 인과분석 방법론을 정립하고 그 상황에서만 해당 인과분석을 빠르게 사용하도록 하는 것이 좋다고 생각합니다. 지나치게 복잡하고 어려운 분석은 회사의 주요 의사결정자를 설득하기에 현실적으로 어려움이 있고, 회사의 주요 의사결정 시기를 지나 내놓는 분석은 쓸모없기 때문입니다. 한편으로는 이런 점에서 성능으로 얘기할 수 있는 머신러닝 딥러닝이 ROI가 높다고 느껴지기도 합니다.
오늘 소개할 그래인저 인과관계 검정(Granger causality test)은 가짜 상관관계(Spurious correlation)을 빠르게 걸러낼 때 사용하기 좋은 방법론입니다. 저도 입사 초기에 이렇게 저렇게 조합해 새로운 지표를 만들고 매출과 상관관계가 높아 “와 이거다!” 했다가, 세상일이 이렇게 쉽지 않을텐데 싶어서 그래인저 검정 돌려 가짜 상관관계였음을 알게 된 적이 있습니다. 스타트업 레벨에서 어떤 지표를 개선할까에 대해 아이디어 낼 때 주요 지표와 상관성이 높은 지표를 보면서 개선할 후보들을 고른다는 아티클 및 강연들을 본 적이 있는데 이런 경우에도 사용해볼만한 방법론이라고 생각됩니다. 상��관성 히트맵에 붉게 나온 대부분의 지표들이 사실 주요 지표에 크게 영향 없을 수도 있으니까요…
그래인저 검정
우선 그래인저 검정은 시계열 데이터에 사용하는 방법론입니다. 근데 다변량 회귀분석과 똑같습니다. 설명을 위해 X(t)와 Y(t)만 있다고 해보겠습니다(Z(t) 등으로 늘리는 건 원리가 같아서 X, Y로 설명한 걸 확장하시면 됩니다).
시간적 선행성
X가 Y에 인과적 영향을 준다는 건 시간 관점에서 보면 X에 변화가 있고나서 Y에 변화가 발생했다라고도 할 수 있습니다. 물론 시간적 선행성만 갖춰진다해서 인과관계가 있다 할 수는 없지만 여러 조건 중에 하나인 것은 맞죠. 그래서 그래인저 검정에서는 과거 시점 X 데이터를 독립변수로, Y를 종속변수로 사용합니다. 식으로 표현하면 Y = a1X(t-1) + a2X(t-2) + … + c 형태가 되겠습니다.
자기회귀 모델
그런데 위 식으로는 선행성은 담아낼 수 있어도 저걸 인과관계라 하긴 어려울 것 같습니다. 사실 Y(t)에 영향준 것이 X(t-n)이 아니라 Y(t-n)이라면 위 식에 Y(t-n)도 추가를 해줘야겠죠. 이를 추가하면 Y = a1X(t-1) + a2X(t-2) + … + b1Y(t-1) + b2Y(t-2) + … + c 형태가 되겠습니다. 설명이 어떤게 더 편할까를 생각해 선행성 -> 자기회귀 순으로 설명했지만 자기회귀가 있다는 게 가장 중요한 가정입니다. 그래서 a값은 이미 0이 아닐테니 b값들이 모두 0인 것이 영가설, b값들 중 최소한 하나 이상이 0이 아닌 것이 대립가설이 됩니다. 해석해보자면 자기회귀로 돌렸을 때 설명력과 비교했을 때 X변수를 추가할 때 설명력이 좋아지지 않는다면 인과성이 있다고 보지 않고, 설명력이 좋아진다면 인과성이 있다고 보는 것입니다. 논리적으로 설득력 있죠?
방향성
식을 보시면 아시겠지만 위 식으로는 X가 Y에 영향을 주는지만 확인 가능합니다. 그래서 일반적으로 방향을 바꿔서 한번씩 한다고 합니다. 그러면 4가지 구조가 형성되겠죠.
- X -> Y
- Y -> X
- X <-> Y
- X 랑 Y 상관 없음
추가 정보
그래인저 검정을 통해 얻은 인과관계를 G-causality라고 흔히 부릅니다.
제가 직접 한 번 해보겠습니다. 으아아아아아아아아아아!!!!
원래 계획은 가짜 상관관계를 모아놓는 사이트로 유명한 spurious correlations에서 데이터를 가져와 돌려보려고 했는데 소스 데이터 링크들이 잘 관리가 안 되고, 페이지 내에서 확인 가능한 값들은 로우 수가 적어서 성에 차지 않아 부동산 가격을 가지고 해봤습니다.
부동산 가격은 누가 이끌까?
일반적으로 부동산 매매가와 전세가는 같이 움직이는 특성을 가지고 있습니다. 그런데 이렇게 같이 움직이는 가격을 해석할 때 두 가지 시선이 갈립니다. 특히 이런 갑론을박은 부동산 상승장에 심하니 상승장이라는 가정 하에 논리를 적어보겠습니다.
- 전세 -> 매매 진영
- 전세가가 올라서 하방 안정성이 높은 지점에 형성되니 매매가가 올라간 것이다 (차익 관점)
- 전세를 통해 얻을 수 있는 은행 이자를 월세라고 생각하면 월세가 올랐으니 수익성이 강화되어 아파트 상품의 가치가 올라 매매가가 올라간 것이다 (수익 관점)
- 매매 -> 전세 진영
- 매매가가 올라 투자한 사람들의 투자금이 높아져 그만큼을 세입자에게 전가해 전세가를 높게 책정하여 전세가가 올라간 것이다.
두 가격은 분명 같이 움직이지만 소위 전문가들 사이에서도 의견이 갈리는 내용입니다. 전문가라고 하려면 기본적으로 데이터는 다 보기 때문에 데이터를 봤다 안 봤다가 중요한 상황은 아닐 것 같습니다. 이렇게 애매할 때 분석가가 투입되어야겠죠.
저는 KB 부동산에서 KB통계 > 월간 통계 > 월간 시계 파일을 다운받아 사용했습니다. 감사하게도 엑셀 파일 버튼 조금만 누르면 원하는 값들을 볼 수 있었습니다. 한국부동산원이 아닌 KB부동산 자료를 활용한 것은 일부 기간 한국부동산원의 정보가 표본이 적어 현실과 동떨어지게 반영되었고 최근에 정상화 되었다는 얘기를 들어서입니다(관련기사).
일단 터무니 없이 예전이지만 1986년 1월부터 시각화 해보겠습니다.
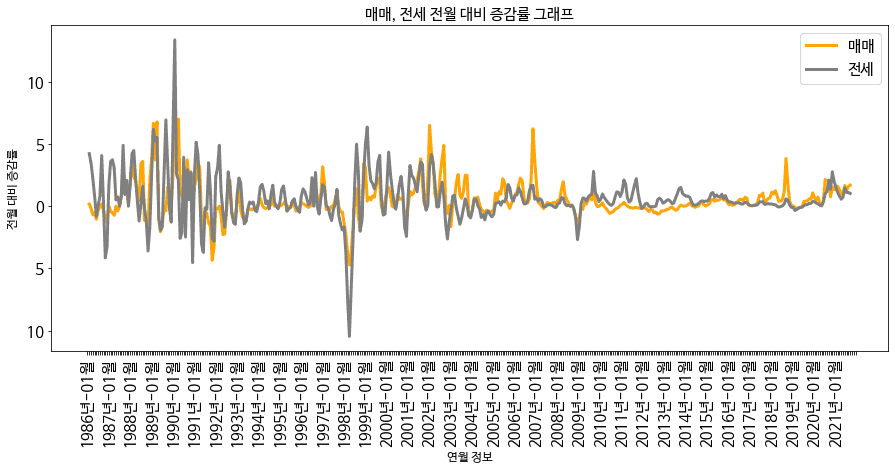
데이터는 서울 지역 매매/전세가 전월대비 증감률인데요, 상당히 비슷한 추세로 움직이는 것을 확인할 수 있습니다. 이제 그래인저 검정을 사용해보겠습니다. 가능한 케이스는 1) 전세가 매매에 영향을 준다, 2) 매매가 전세에 영향을 준다, 3) 서로 영향을 준다, 4) 아파트 공급, 금리 같은 제3의 교란 변수가 있어 서로 영향이 없다 이렇게 네가지겠네요.
데이터 가공
다행히 데이터가 증감률 형태여서 거의 바로 활용할 수 있었습니다. 혹시 가지고 계신 데이터가 증감률 형태가 아니라면 몇 가지 가공이 필요할 수 있습니다. 우선 정상성(stationarity)가 충족되어야 합니다. 정상성이 없는 시계열 데이터를 정상성 있는 데이터로 만들기 위해서는 일반적으로 차분과 로그 변환을 많이 하는데요, 특히 경제학을 공부해보신 분들은 친숙할텐데 증감률은 절대값이 심하게 크지 않는 한 로그 차분에 근사하는 수치입니다. 그래서 저는 별도로 정상성을 만들기 위한 작업을 하지 않았습니다. 만약 여기서 다룬 용어들이 낯설게 느껴지신다면 이 블로그를 추천드립니다.
증감률 형태이긴 하지만 혹시 몰라 ADF와 KPSS 테스트를 진행하였고 정상성이 있다고 판단해도 될 것 같아 진행시켰습니다.
전세가와 매매가의 영향
p-value가 유의성 기준을 0.05로 뒀을 때, 0.05 미만이면 정확한 의미는 'x가 y에 영향을 주지 않는다고 할 수 없다'이지만 말이 직관적이지 않은 관계로 'x가 y에 영향을 준다'로 표현하겠습니다.본 분석은 학술연구가 아닌 그래인저 검정을 설명하기 위해 데이터에 적용해보는 것이니 신뢰성이 떨어질 수 있습니다.
데이터를 통째로 넣고 진행했을 때 안타깝게도(?) 서로 영향을 주는 것으로 나왔습니다. 위 3) 서로 영향을 준다 케이스가 된 거죠. 생각보다는 서로의 가격에 영향을 주는 시점이 빠르게 나타났습니다. 전세 -> 매매는 4개월부터, 매매 -> 전세는 2개월부터 영향을 주었습니다. 그런데 1986년부터 2021년까지 서울의 부동산 특성이 다양하게 변해왔을텐데 한 번에 다 넣고 돌리는 게 맞을까라는 생각이 들었습니다. 1980년대는 지금과 달리 아파트가 막 지어지던 시기였는데 성격이 비슷하다 보기 어려울 것 같고 상승장 하락장마다 영향력도 다를 수 있을 것 같았거든요. 그래서 상승장, 하락장, 횡보장으로 나누어 각 시장 상황마다 그래인저 검정을 진행해봤습니다(이렇게 제 맘대로 기간을 쪼개도 되는건지까지는 솔직히 모르겠지만 일단 너그러이 이해를…).
- 상승장
| 시기 | 그래인저 테스트 결과 |
|---|---|
| 1980년대 (1986~1989) | 4) 서로 영향이 없다 |
| 2000년부터 2008년 | 1) 전세가 매매에 영향을 준다 |
| 2013년부터 현재 | 4) 서로 영향이 없다 |
- 하락장
| 시기 | 그래인저 테스트 결과 |
|---|---|
| 1997년부터 1999년 | 3) 서로 영향을 준다 |
| 2009년부터 2012년 | 2) 매매가 전세에 영향을 준다 |
- 횡보장
| 시기 | 그래인저 테스트 결과 |
|---|---|
| 1990년부터 1996년 | 3) 서로 영향을 준다 |
해설을 해보자면,
- 3번의 상승장 중 2번은 서로 영향이 없다(=매매 및 전세가를 올리는 외부 공통 요인이 있다)였고, 1번은 전세가 상승이 매매가를 끌어올렸다
- 2번의 하락장 중 1번은 서로의 가격이 서로에 영향을 주었고, 1번은 매매가의 하락이 전세가를 끌어올렸다
- 1번의 횡보장 때는 서로의 가격이 서로에 영향을 주었다.
이렇게 볼 수 있겠습니다.
직접 해보고 느낀 점
spurious correlations 사이트 데이터로 가볍게 하려던 게 부동산 데이터를 정해버리는 바람에 제 능력 대비 어려운 주제를 다루었는데요, 실제 데이터에 적용하려니 기간을 어디부터 어디까지 설정할 것인지가 가장 어려웠습니다. 아마 현업에 적용하려 해도 이런 기간을 정하고 데이터 포인트를 일 단위로 할지 월 단위로 할지 같은 것을 정하는 게 가장 어려운 포인트가 될 것 같습니다. 한편으로는 그 외의 것들은 크게 고려하지 않았을 정도로 그래인저 검정이 얼마나 간편한지 느낄 수 있었습니다. 특히 시계열 특성상 데이터가 많지 않아도 적용 가능한 방법론이라 많은 회사, 개인이 시도해볼 수 있을 것 같습니다. 추가로 다시 한 번 도메인 지식의 중요성을 생각하게 되었습니다.
