이 글은 작성자 블로그에서도 보실 수 있습니다.

Intro

1. 잠재요인 분석 (Factor Analysis)

• 잠재요인 분석은 관찰되는 데이터들을 설명할 수 있는 몇 가지 잠재적인 요소(latent factor)가 있다는 데에서 출발한다. 간단한 예로 는 여러과목(국,영,수, 사회, 과학 등의 과목)의 성적을 관찰하면서 여러 과목에 걸쳐서 공통된 어떤 요인(논리능력, 암기력 등) 이 있는지를 알아내는 경우이다. 데이터 포인트가 많아질 수록 전체를 설명할 수 있는 공통된 요소를 찾아낸다는 점에 있어서는 각 독립변수들에 대하여 직교하는 성질을 가지는 주성분으로 분해하는 PCA(주성분분석)와도 유사한 점이 있다. 차이점이라면 주성분 분석이 직교 성질을 반드시 만족하는 방식으로 독립변수와 동일한 수의 주성분을 찾아간다는 것이고, 잠재요인 분석에서는 주요 성분들을 직교 성질과 무관하게 그리고 독립변수의 개수보다 더 적은 변수를 찾아간다는 점이다.

2. 유래

• Spearman’s rank correlation coefficient 로 유명한 통계학자이자 심리학자였던 Charles Spearmen이 지능에 대한 잠재 요인을 찾기 위해 1904년 고안하였다. 잠재요인분석이라는 주제는 통계학책에서 보통 가장 마지막 챕터쯤에 나오기 때문에 잘 들여다보기 힘든 내용이다. 하지만 PCA, MLE, Regression 등 통계의 여러가지 개념과 연결이 되는 흥미로운 주제다.

3. 용어

• 잠재요인분석에 대한 대략적인 개념과 용어를 이해하기 위해서는 심리학에서 자주 사용되는 battery test에 대한 묘사로 설명하는것이 용이하다. battery test는 여러가지 세부 테스트로 구성되어서 점수화 될 수 있는데 이 목록들에는 어휘력, 기억력, 연상력(analogies), 수리 추론(math reasoning), 공간 조작능력(spatial manipulation)들이 있다. 그리고 우리는 이 항목들에 대한 기저 능력들이 있을 것이라고 가정해볼 수 있다. 이 기저 능력을 요인 G이라고 하고, 요인들은 여러 테스트 점수에 공통적으로 영향을 미치는 것이어야 한다. 테스트 점수 자체는 독립변수이자 manifest variables 라고 하고 관찰되지 않는 요인 G는 공통요인 혹은 latent variable(잠재 변수), hidden variable 이라고 부르기도 한다.

공식과 가정

• 잠재요인 분석(FA)의 구성 모델은 아래와 같다.

• 가정(Assumption)

잠재요인분석에는 다음과같은 가정들이 필요하다.

1. 독립변수가 p개 존재할 때, $ X_1, X_2, \cdots, X_p $ 공통 요인들은 m의 개수만큼 존재한다. $\xi_1,\xi_2,\xi_3,\cdots,\xi_p$ $(p > m)$
2. 각각의 독립변수 $X$ 는 m 개의 공통 요인들의 선형 결합으로 표현할 수 있으며 선형결합으로 표현되지 않은 나머지 요소들이 고유 요인 $\epsilon$ 으로 남는다.
3. 공통요소는 반드시 최소한 두 개 이상의 독립변수에 영향을 미칠 수 있어야 한다. 만약 하나의 독립변수만을 설명할 수 있다면 공툥요소가 아니라 고유요소가 되어야 한다. (즉, 적어도 두개 이상의 $\lambda$ 는 0이 아니다.)
4. 모든 $i, j$ 에 대하여 $corr(\epsilon_i, \epsilon_j)=0$. 두개 이상의 고유요인들간에 상관관계가 있다면 고유요인에 대한 정의를 위반한다.
5. 모든 $i, j$ 에 대하여 $corr(\xi_i, \epsilon_j)=0$. 공통 요인의 정의는 최소한 두 가지 이상의 독립변수에 영향을 미치기 때문에 고유요인인 $\epsilon$과의 상관성이 존재해서는 안된다.
6. (Optional) 모든 $i, j$ 에 대하여 $corr(\xi_i, \xi_j)=0$. 이 가정은 모든 공통 요인들이 서로 독립이어야 한다는 가정으로 이 가정은 PCA의 주성분에 관하여는 항상 맞는 가정이지만 FA(잠재요인분석)에서는 반드시 요구되는 것은 아니다.
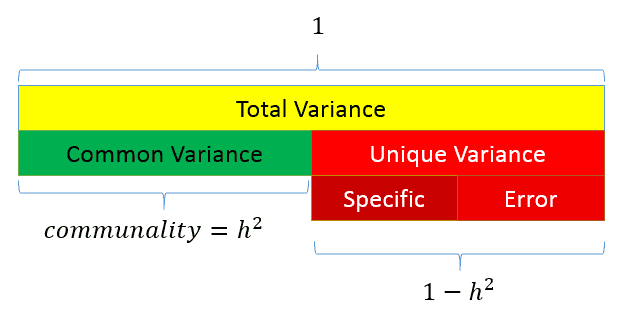
   변수에 대한 분산의 관점에서 정리하면 아래와 같이 단순화할 수 있다. 모든 독립변수 $X_i$ 는 공통요인과 고유요인의 합으로 이루어진다 식으로 단순화하면,

와 같다. $\lambda_{ij}$ 는 $corr(X_i,\xi_j)$ 로 정의되어서 $\lambda_{ij}^2$ 은 R-squre ($X_i$를 설명하는 분산의 비율)가 된다. 도식적으로 표현할 수도 있다.

분석사례

본 예제는 SaS 툴에서 진행되었습니다. 하지만 Python이나 R, SPSS 어떤 것이든 Factor Analysis를 할 수 있으며 특히 Scikit Learn에는 Factor Analysis 클래스가 존재합니다.

여기 슈퍼바이저에 대한 평가점수가 있다. (데이터보기) 7개의 컬럼 중에 첫번째 항목인 종합평가점수(OVERALL)과 함께 총 6가지 평가 항목이 있으며 FA(잠재요인분석)의 목표는 6가지 평가 항목에 대한 공통 요인의 개수 찾아내고 그 요인에 대한 적절한 설명을 붙여주는 것이다.

6가지 항목은 각각 불만수용(BEEFS), 자율성(PRIVILEGE), 자기계발(NEWLEARN), 공평한 승진(RAISES), 비난(CRITICAL), 새로운 기회 제시(ADVANCE) 이다.

FA를 모델링은 두 가지 스타일로 진행하였다. 먼저 PCA 스타일로 진행하고 그 다음에 SMC¹스타일로 진행하였다.

1. PCA 스타일

• FA에 대해서 어떠한 고유 요인($\epsilon$)을 남겨두지 않고 직교성질을 만족하는 6개의 Factor를 모두를 추출해내는 방식이다. 기본적으로 PCA와 다르지 않다.

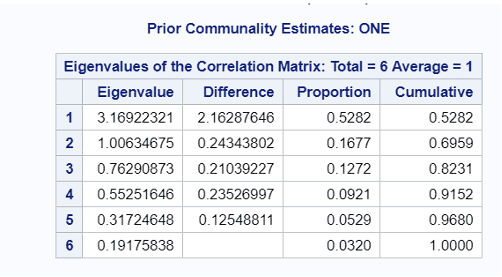
6개의 주성분을 모두 추출하였고, Eigenvalue(주성분의 중요도) 기준으로 누저적으로 82.31%의 설명력을 가지는 Factor1, Factor2, Factor3가 중요하다는 것을 확인할 수 있다. Factor1은 모든 변수에 대하여 무려 52.82%를 설명하고 있다.

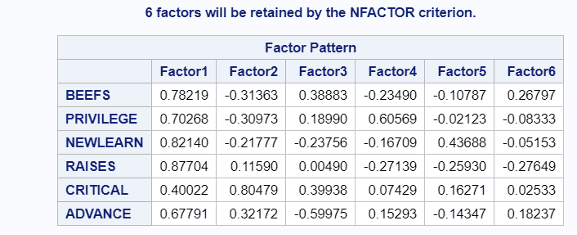
Factor1을 해석해보면 6가지 항목 중 비난(Critical)이 약간 낮은 상관성을 가지는 것을 제외하면 나머지 5가지 독립변수가 꽤 강한 강도를 가지고 있다는 것을 볼 수 있다. Factor2에 대해서는 강한 설명력을 가지는 변수가 비난(Critical)인데 나머지 독립변수들은 Factor2에서 상대적으로 덜 중요한 설명력을 가지고 있는 것을 볼 수 있다. 이제 두 요인에 대한 해석을 해볼 수 있다. Factor1이 일반적으로 생각되는 좋은 매니저로서의 자질을 설명하고 있다면 Factor2에서는 직설적이고 비판적인 성향을 가진 매니저가 구분될 수 있다는 사실을 의미한다. PCA 방식으로 FA를 진행했기 떄문에 Factor1과 Factor2는 직교성질을 가진 독립적인 factor이므로 매내저를 설명하기 위한 서로 다른 factor로 바라보아도 좋을 것이다.

2. SMC 스타일

• PCA 방식으로 FA를 진행하면 사실상 공통요인(communality)는 100%이기 때문에 고유요인이 존재하지 않는다. 이런 가정은 실제로 모든 변수들에 대해서는 공통요인으로 설명할 수 없는 고유요인이 존재할 수 있다는 잠재요인분석의 기본적인 아이디어와 반대되기 때문에 squared multiple correlation 스타일에서는 communality의 크기를 추정하는 방식을 사용한다. Regression의 아이디어를 사용하는 이에 대한 자세한 설명은 참고문서 1 에 남겨두기로 하고 먼저 분석 결과를 보자.

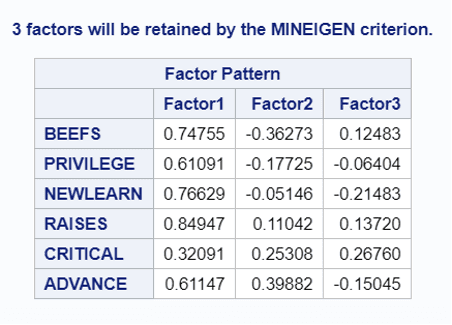
• SMC 스타일로 진행한 경우 6개의 factor를 모두 추출하는 것이 아니라 기준을 충족하는 상위 3개의 factor만을 추출하였다. 전체적으로 Factor1에 대한 의미는 PCA 방식으로 진행한 경우와 큰 차이는 없어 보인다. 역시 비판 (Critical)이 Factor1에 대해서는 낮은 설명력을 가진다는 점도 유사하다. 하지만 Factor2의 의미는 약간 바뀌었는데 비판에 대한 설명력은 줄어들고 새로운 기회 제공(Advance)에 대한 양의 설명력과 함께 불만수용(BEEFS)에 대해서 음의 설명력을 보인다. Factor2에 대한 새로운 해석은 이야기를 잘 들어주거나 하는 일반적인 미덕보다는 조금 더 진취적인 기회나 미래를 제시할 수 있는 리더의 이미지에 가까워 보인다.

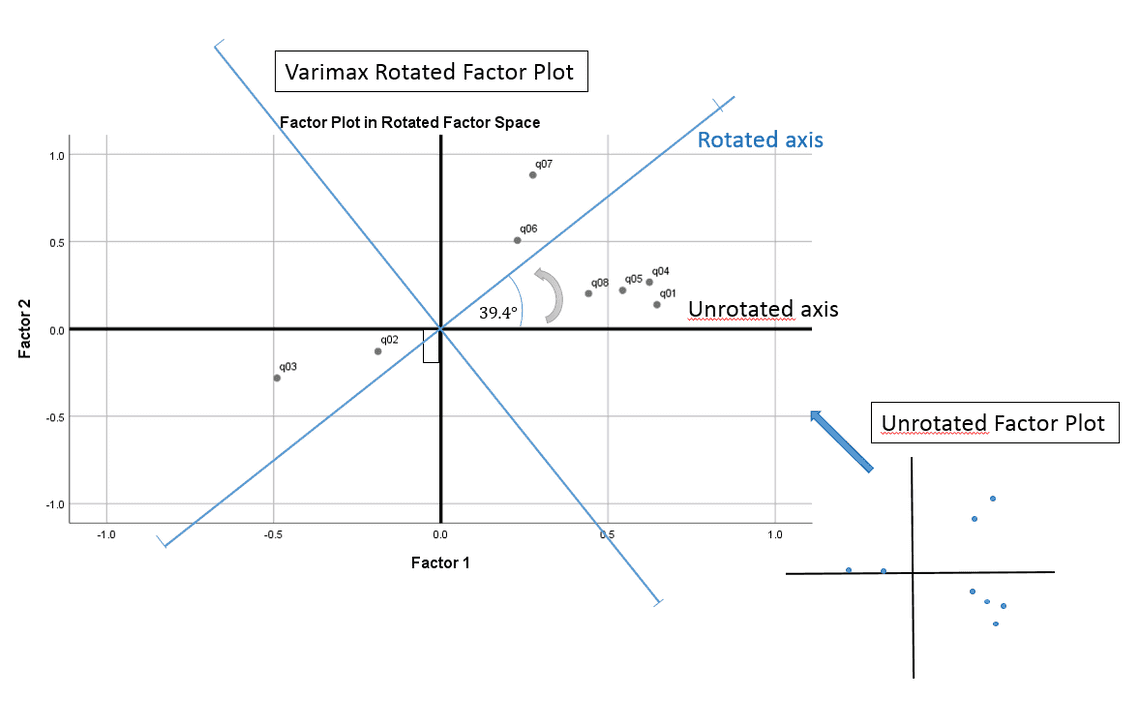
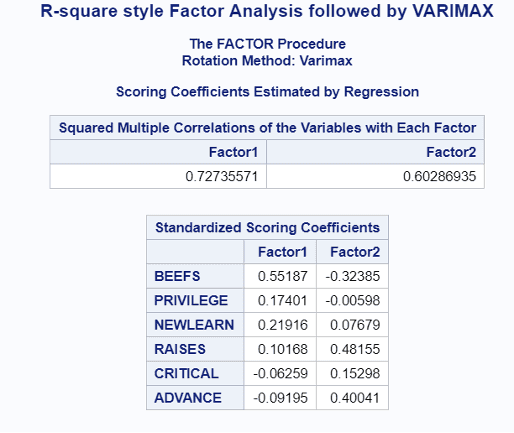
• 마지막으로 이번에는 2개의 Factor만 추출을 해보기로 한다. 앞에서 3개의 factor를 추출하기 위해 사용한 smc 방법에 더하여 추가적으로 VARIMAX²라는 변형을 적용하는데, 이는 분산(Variance)를 최대한으로 만들어주는 rotation 기법으로 역시 직교성질을 만족시킨다는 점에서 PCA(주성분분석)와 유사한 개념이다. 그림에서 나와있듯이 Factor1과 Factor2의 SMC는 각각 0.73, 0.60으로 높은 수준으로 추출되었음을 확인할 수 있다. 또한 2개의 Factor에 대한 해석을 해보면 이전과는 약간 달라진 것을 볼 수 있다. Factor1은 이전과 달리 일반적으로 좋은 매니저의 장점을 골고루 갖추었다기 보다는 불만 수용(BEEFS)와 약간의 자기계발 성향(NEWLEARN)등 전반적으로 자상한 느낌의 성향이라 볼 수 있을 것이고, Factor2는 공평한승진(RAISES), 새로운기회제공(ADVANCE) 등 공적인 부분에서 능력을 보여주는 유능한 매니저의 성향으로 해석해볼 수도 있을 것 같다.

결론

Factor Analysis는 전반적으로 PCA와 유사한 방법론을 가지고 있지만, 사용 목적과 관점이 크게 다르다. PCA가 직교성질을 가진 독립적인 성분을 분해해내는데 집중한다면, Factor Analysis는 공통요인을 찾아내는 것이 목적이다. 그렇기 때문에 직교성질이 가끔 위배될 수도 있는 것이다(가정 6의 완화). 같은 맥락에서 공통 요인의 전체적인 크기를 찾아내는 것에 대한 여러가지 가정(PCA 방식, SMC 방식 등) 이 존재하고, 여러가지 변환도 할 수 있다(VARIMAX 변환 등). Factor Analysis는 여전히 선형 결합이기 떄문에 선형 모델이 가지고 있는 한계도 동일하게 가지고 있다. 하지만 비선형 모델의 경우 오히려 해석력이 떨어진다는 점에서 선형모델의 장점도 가지고 있다고 볼 수 있다.

가장 중요한 것은, 위에서 여러가지 방법을 썼다는 점이다. 앞서 말한 것처럼 PCA,SMC 가정 이외에도, Maximum Likelihood, Heywood, Ultraheywood 같은 다양한 가정과 변환 기법에 따라 잠재 요인의 값이 변하면서 자연스럽게 해석이 달라지는데(위의 사례처럼) 어떤 해석이 가장 좋은 것인지 판단하기가 어렵다. 분석가가 사전적으로 공통요인에 대한 가정을 무엇으로 바라보는가에 달려있다고 볼 수 있을 것이다(SMC 가정을 사용한다면 한 변수가 다른 변수들에 의해서 얼마나 설명될 수 있는지를 Regression의 관점에서 가정하는 등).

참고 문서

1. https://stats.oarc.ucla.edu/spss/seminars/introduction-to-factor-analysis/a-practical-introduction-to-factor-analysis/