시계열 분석의 기초는 과거의 관측값이 가지고 있는 여러 패턴 토대로, 미래의 관측값을 예측하는 것입니다. 지난 1편 패턴 쪼개기 글에서는 시계열 데이터를 구성하는 세 가지 구성 요소와 이를 어떻게 나누어서 볼 수 있는지에 대해 다루었어요. 이번 편에서는 시계열 분석 모델의 기초가 되는 정상성(Stationarity)과 자기상관(Autocorrelation)에 대해 풀어 보겠습니다.

이 글은 작성자의 개인 블로그에서도 확인할 수 있습니다.

정상성이 왜 중요한가요?

시계열 분석의 여러 전통적인 모델은 정상화된 시계열을 가정하고 있습니다. 정상성을 가진 데이터는 여러 구간에 걸친 관찰값 간의 관계가 일정하게 정의되기 때문입니다. 현실에서는 두 개를 초과한 시간 구간 간 관계를 명확하게 도출하는 것이 매우 어렵습니다. 따라서 두 시간 구간의 관계를 확인하고, 그것이 다른 구간에도 동일하게 적용된다고 가정하는 것이 모델은 만드는 경제적인 방식인 것이지요. 좀 더 쉽게 풀어볼게요.

과거 관찰값을 바탕으로 미래를 예측하기 위해서는 수집된 관측값이 안정적으로 유지되고 있는 상태인지, 또는 계속해서 변동하는 상태인지를 확인해야 합니다. 이 때, 시계열의 안정적 수준이 바로 “정상성(Stationarity)”이며, 정상이란 변하지 않고 일정한 상태를 의미합니다. 여기서 일정한 상태란, “평균 a에서 위 아래로 b 구간 사이에서 일정하지만 불규칙적인 변동을 가지고 움직이고 있음”을 뜻해요. 정상성을 나타내는 시계열은 시간 축의 어느 구간을 관찰하든 유사한 형태를 보이게 되며, 규칙이 없는 상태이기 때문에 예측이 불가합니다.

먼저 시계열의 안전성을 측정 했다면, 이어서 시계열 관측값이 가지고 있는 변동성을 추가적으로 파악할 수 있습니다. 간단히 이야기해서 시계열 관측값이 안정적인 상태일 때 가지는 평균과 분산을 파악하고, 여기에 지난 시간에 함께 알아보았던 추세와 계절성 등의 성분을 한 층씩 더해 예측 값을 만들어 내는 것이지요. 이 변동성이 오늘 설명할 개념 중 하나인 자기상관과 이어집니다. 미래 관측값 예측에 과거의 데이터가 얼마나 밀접한 연관성을 가지는지 알 수 있게 해주는 척도이기 때문입니다.

자기상관(Autocorrelation)의 기본 개념

두 변수 사이의 선형 관계를 측정하는 ‘상관관계’는 이 글을 읽고 계신 분들께는 꽤나 익숙한 개념일 거에요. 이와 유사하게 자기상관은 시계열의 시차값(Lagged Values) 사이의 선형 관계를 측정하는 개념입니다. 오늘(t)와 어제(t-1), 오늘과 그제(t-2), 또는 오늘(t)과 일주일 전(t-7)과 같이 현재 값과 지연 값을 비교함으로써, 과거의 관찰값이 현재 관찰값에 얼마나 영향을 미치는지 직관적으로 확인할 수 있습니다.

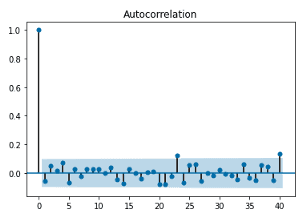
자기상관은 ACF(Autocorrelation Function)을 통해 시각화합니다. 아래 그림을 보면 ACF 그래프의 x 축은 (지연된) 시차를 나타내고, y 축은 상관계수를 보여줍니다. 시차가 0일 때 모든 시계열의 자기상관계수는 1이며, 정상성을 띠는 데이터는 2부터 n차 지연까지의 자기상관계수가 0에 가깝게 나타납니다. 그림에서 하늘색으로 표시된 영역은 신뢰구간을 의미하고요. 아래 경우는 일부 시차를 제외하고 자기상관계수가 대체로 0에 가깝게 위치하고 있어요.

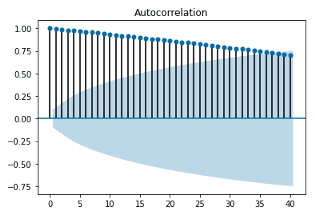
반면 다음 ACF 그래프는 거의 모든 시차에 대해 자기상관계수가 허용 범위를 초과하고 있습니다. 이 경우 관찰값은 비정상적(Non-stationary)이며, 시차가 커질 수록 자기상관계수가 점진적으로 줄어드는 형태를 보이는 것은 시간이 지날 수록 데이터 간의 자기 상관이 감소한다는 것을 보여줍니다. 즉, 어제의 데이터가 오늘을 가장 잘 설명하고, 일주일, 한달, 과거로 갈 수록 데이터의 상관성은 상대적으로 낮아진다는 의미입니다.

White Noise와 Random Walk

White Noise는 일정한 규칙 없이 전체적이고 일정한 범위를 가진 상태로, 대표적으로 정상성을 나타내는 시계열입니다. 아래 1,000개의 Random 관측값을 나열한 그래프를 통해 직관적으로 이해할 수 있습니다.

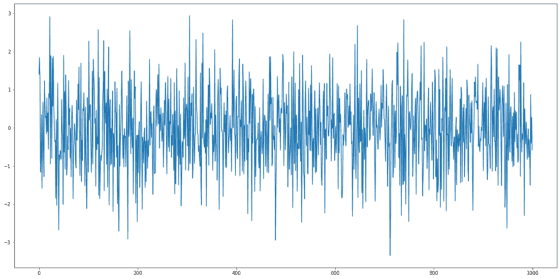
White Noise는 다음 세 가지 전제 조건을 가지고 있어요 :

• 평균이 일정하다.
• 분산이 일정하다.
• 관측값 간의 상관관계가 없다. (유의하지 않다)

글 초입에 ‘정상화된 시계열은 예측이 불가하다’고 설명했는데, 이는 어떤 값을 예측했을 때 그 결과의 잔차(실제값과 예측값의 차이)가 White Noise의 형태를 띠고 있다면, 해당 예측 모델은 최적화된 상태라는 의미합니다. 더 이상 예측이 불가한 상태까지 패턴이 모두 추출되어 모델에 반영되었기 때문이에요.

Random Walk는 White Noise에서 한 단계가 더해진 개념으로, 사전적 정의는 ‘임의 방향으로 향하는 연속적 걸음’ 이에요. 임의라는 단어에서 알 수 있듯이 Random Walk 또한 예측이 불가하지만, White Noise와 다른 부분은 Random Walk이 직전의 관찰값에 기초한다는 점이에요. 이 개념은 주식 가격의 움직임을 설명하는 데에 자주 사용되는데, “오늘의 주가 = 어제의 주가 + Noise”로 간단히 나타낼 수 있습니다. 이 때, 어제의 주가에 더해지는 Noise가 바로 White Noise에 해당합니다.

아래는 간단한 Random Walk 모델을 Simulation한 결과입니다. 초기 값을 1,000으로 두고, 위에서 만들어둔 White Noise를 활용했어요.

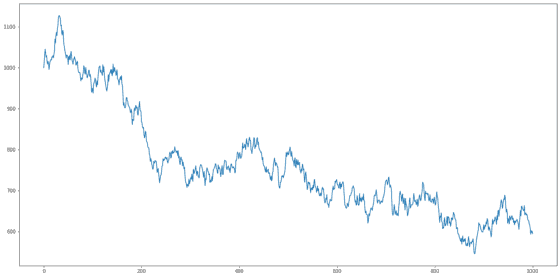
Random Walk 모델은 비정상적이며, 통상 긴 주기로 보았을 때 상향 또는 하향하는 추세를 가지고, 갑작스럽고 예측할 수 없는 방향 변화를 보입니다. Random Walk는 쉽게 정상화할 수 있는데, 다음의 변형된 수식을 보면 간단히 알 수 있습니다 : “오늘의 주가 — 어제의 주가 = Noise” 즉, 오늘 주가(t)에서 어제 주가(t-1)을 빼주면 되는데, 이를 차분(Difference)이라고 합니다.

정상성의 정의와 평가

정상성을 둘러싼 여러 기초 개념을 설명했으니, 이제 다시 먼 길을 둘러 정상성의 이야기로 돌아와 볼게요. 시계열 데이터가 정상성을 띤다는 것은 “데이터의 분포가 시간에 따라 변하지 않는다”는 의미이며, 세 가지 기준으로 이를 판단할 수 있습니다 :

• 트랜드가 없다 (오르거나 줄어들지 않는다)
• 분산이 일정하다
• 자기상관이 일정하다

어떤 데이터가 정상성을 띠는지 평가하는 방법은 여러 가지가 있습니다. 먼저 정확하지는 않지만, 가장 쉽게 접근할 수 있는 방법은 시각화입니다. 다음 아홉 가지 시계열에서 어떤 것이 정상성을 나타낼까요?

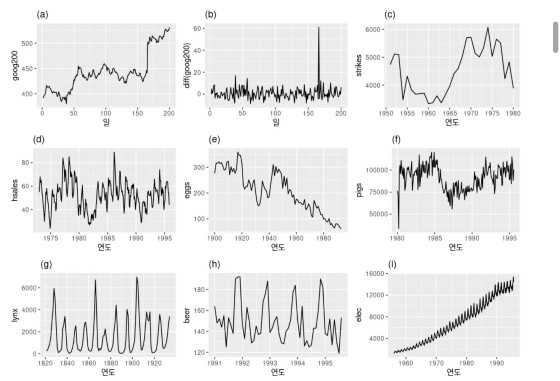
분명하게 계절성이 보이는 (d), (h), (i)는 후보가 되지 못합니다. 추세가 있고 수준이 변하는 (a), (c), (e), (f), (i)도 후보가 되지 못합니다. 분산이 증가하는 (i)도 후보가 되지 못합니다. 그러면 (b)와 (g)만 정상성을 나타내는 시계열 후보로 남았습니다.

이 예시와 정상성 분류에 대한 설명은 롭 힌드만과 조지 아타나소풀로스 교수의 저서 “Forcasting : Principles and Practice” 의 번역본 원문을 그대로 참조 했습니다. 설명의 흐름을 보면, 한 번에 정상성을 찾아내기 보다 비정상성을 제외 하는 방식을 따라가고 있습니다. 실제로 정상성을 정확하게 정의하는 것보다, 비정상을 배제하는 것이 보다 직관적인 방법입니다.

시각적으로 정상성을 판별하기 불분명한 경우가 있습니다. 이때는 측정 가능한 방식으로 정상성을 판별하기 위해 가설 검정을 활용할 수 있는데요. 오늘은 여러 방법 중 보편적으로 활용 되는 Augmented Dickey-Fuller (ADF) 검정에 대해 간단히 정리하겠습니다. ADF 검정은 단위근(Unit Root)의 유무를 기준으로 정상성을 판별하는데, 기본적으로 단위근이 있는 시계열은 비정상 입니다. (단위근의 정의와 단위근이 있을 때 시계열이 비정상인 이유가 궁금하다면 ritvikmath의 Unit Root 영상을 추천합니다.)

ADF 검정의 논리를 간단히 설명하면 :

• ADF는 기본적으로, 시계열에 단위근이 존재한다고 가정합니다. 즉, 시계열이 비정상적이라고 가정합니다.
• 검정 결과 귀무 가설이 기각된다면 ( = p-value가 유의수준 보다 작다면) 대상 시계열은 정상으로 판단 될 수 있습니다.
• 검정 결과 귀무 가설이 기각되지 않는다면 대상 시계열은 비정상으로 판단 됩니다.

정상성에 대한 이야기를 시작하면서 ‘시계열 분석의 여러 전통적인 모델은 정상화된 시계열을 가정’하고 있다고 말씀 드렸습니다. 그렇지만 현실에서 우리가 분석하고자 하는 많은 데이터는 정상성을 띠고 있지 않을 거에요. 그래서 시계열 분석을 위해서는 몇 가지 간단한 조작을 통해 비정상 데이터를 정상으로 변환하는 과정이 필요합니다.

정상 변환 (feat. 애플 AAPL 주가)

비정상 시계열을 정상 시계열로 변환 과정에 대한 이해와 함께 오늘 설명한 여러 내용을 복습하기 위해, 제가 가장 애정하는 애플(AAPL)의 주가 데이터를 활용해서 실습을 진행해 보아요.

먼저, 시계열 정상 변환을 위해 알아야 하는 기본 규칙은 다음과 같습니다 :

• 변동폭이 일정하지 않을 때는 로그 변환으로, 분산이 일정하게 유지되도록 만들기
• 추세 또는 계절적 요인은 차분을 통해 평균이 일정한 시계열로 변환하기

그럼 이제 본격적으로 애플 주식을 불러와 볼게요. 이번 실습에서는 애플의 일별 종가를 활용하는데, 데이터 로딩에 yfinance 라이브러리를 사용했습니다.

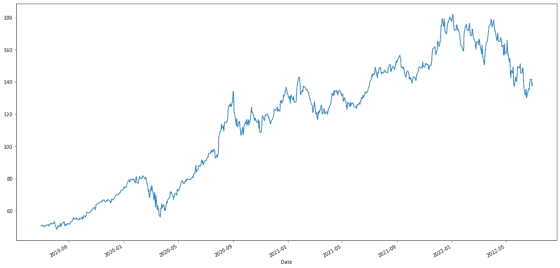
2019년 하반기부터 2022년 상반기까지 3년 간 주가 흐름을 보면, 시간에 따라 주가 변동폭에 차이가 있습니다. 2019년 하반기 — 2020년 상반기 대비 이후 기간의 주가가 보다 큰 폭으로 움직이고 있는 것 같네요. 로그 변환이 필요할 것 같습니다. 뿐만 아니라, 주가가 우상향 하는 추세를 제거하기 위해서는 차분 과정도 필요합니다.

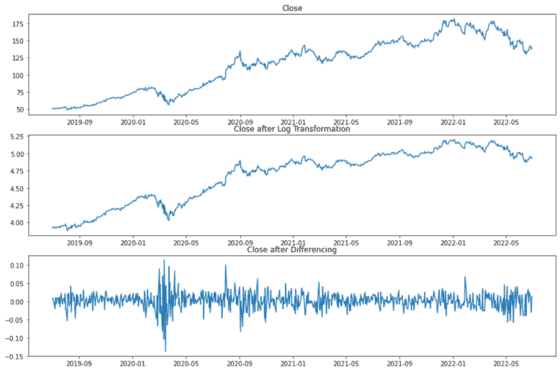
순서대로 애플의 종가, 로그 변환 결과, 로그 변환에 차분을 적용한 결과입니다. 세 번째 그래프를 보면 제법 정상성을 띠는 것처럼 보입니다.

• ADF Statistic : -8.863
• p-value : 0.000
• Critical Values : {‘1%’ : -3.439, ‘5%’ : -2.865, ’10%’ : -2.569}

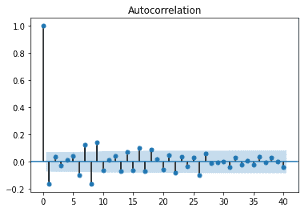
정확한 판별을 위해 ACF와 ADF 검정 결과도 함께 살펴 보았습니다. ACF 그래프는 일부 시차를 제외하고 자기상관계수가 대체로 0에 가깝게 위치하고 있습니다. ADF 검정 결과 p-value는 0에 근사한 값으로, 귀무 가설을 기각하여 정상성 변환이 정상적으로 이루어 졌음을 확인할 수 있습니다.

정상성까지 배웠으니, 이제 멀고도 험한 예측의 산을 오를 준비가 끝났습니다. (준비만 한 세월 😵) 다음 번에는 시계열 예측에 활용되는 기본 모델에 대한 글을 가지고 올게요. 잊지 말고 기다려 주세요. 그럼 다시 만나요!

Reference

• Dario Radečić (2021) Time Series From Scratch — White Noise and Random Walk. https://towardsdatascience.com/time-series-from-scratch-white-noise-and-random-walk-5c96270514d3?gi=90fdbb451b31.
• Hyndman, R.J., & Athanasopoulos, G. (2018) Forecasting: principles and practice, 2nd edition, OTexts: Melbourne, Australia. OTexts.com/fpp2.
• ritvikmath. (2020) Unit Roots : Time Series Talk. https://youtu.be/ugOvehrTRR.
• Eunji Lee. (2021) 시계열 분석 시리즈 (1): 정상성 (Stationarity) 뽀개기. https://assaeunji.github.io/statistics/2021-08-08-stationarity/.