지난 2월 데이터 분석 컨퍼런스 팝콘에서 쉽게 설명하는 분석 개념을 테마로 <다짜고짜 배워보는 인과추론>이라는 제목의 발표를 했습니다. 이번에는 “시계열 분석”을 주제로 다짜고짜 배워보는 시리즈를 이어가 볼게요. 시계열 분석 1편에서는 시계열 분석이란 무엇인지, 그리고 관련된 여러 모델 중 시계열 분해(seasonal decomposition)에 대해 알아보기로 해요!

이 글은 작성자의 개인 블로그에서도 확인할 수 있습니다.

시계열 분석이란?

“미래 예측을 목적으로 시간 정보가 포함된 데이터를 활용하는 분석 방법”

시계열 분석(time series analysis)는 말 그대로 시간의 흐름에 따라 기록된 데이터를 분석하는 방법론입니다. 연간, 월간, 주간, 시/분/초 등 일정한 시간 간격으로 기록된 관측값을 활용해서, 측정치의 변동(movement)을 분석하고, 앞으로 어떻게 움직이게 될지 예측 합니다. 대표적인 시계열 데이터로 주식 가격, 주가 지수와 같은 금융 데이터가 많이 언급되지만, 이 외에도 일별 매출 추이, 특정 검색어에 대한 검색량 변동 등 무궁무진한 활용 사례를 생각해볼 수 있어요.

시계열 데이터를 어떻게 쪼갤 수 있나요?

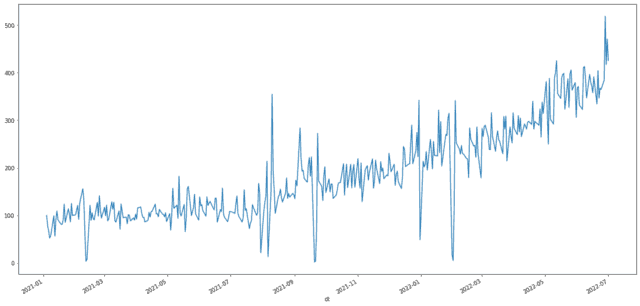
위 그래프는 어느 기업의 일 매출을 나타내고 있습니다. (random하게 만들어진 가상의 데이터로, 2021년 첫 영업일의 매출액이 100이 되도록 조정했어요.) 이 데이터를 보고, 매출 추이를 설명해 본다면 어떨까요? 전반적으로 우상향하는 형태를 띄고 있지만, 중간 중간 정확히 알 수 없는 요인으로 인해 변동이 아주 크게 발생하는 지점이 몇 곳 있네요.

이제 일 매출 추이를 시계열 분석의 관점에서 설명 해볼게요. 시계열 정보는 일반적으로 추세 성분(trend component), 계절 성분(seasonal component), 불규칙 성분(irregular component)으로 구성되며, 관측값의 움직임을 이 성분으로 나누어서 설명합니다. 추세는 관측값의 전반적 상승 또는 하락 경향을 나타내는 성분입니다. 위에서 “전반적으로 우상향 하는 형태”가 바로 추세에 해당합니다. 반대로, 불규칙 성분은 특정한 규칙으로 설명할 수 없는 오차(error)를 나타내는 성분이에요. 마치 우리가 매출 상승에 대한 전반적인 추세를 알고 있어도 내일 매출을 정확히 알 수는 없듯이, 불규칙 성분은 정확히 예측할 수 없는 오차의 영역에 해당합니다. 여기에 추가로, 시계열 데이터가 특정 주기에 따라 일정하게 변동할 때, 이 변동을 설명하는 요인이 계절 성분입니다. 위 그래프에서 매출이 특정 일자에 크게 튀어 오르거나, 갑자기 낮아지는 행태가 공휴일 등의 영향으로 매년 정기적으로 발생한다면, 이 부분에 대한 변동을 계절 성분으로 설명할 수 있는 것입니다.

추세 꺼내보기

먼저, 추세 성분 측정을 위해 가장 기본적으로 사용하는 방법은 이동평균(moving average)입니다. 이동평균은 특정 기간(k) 내의 시계열 평균을 계산하는 방법으로, 많은 분들께 익숙한 평활(smoothing)법일 것이라 생각됩니다. 위의 매출 데이터를 활용해서 추세 성분을 분석 해볼게요.

이동평균을 구하면, 데이터 양 끝의 (k-1)/2개의 관측값이 계산에서 제외되기 때문에, NaN이 포함된 행은 제외 해주었어요.

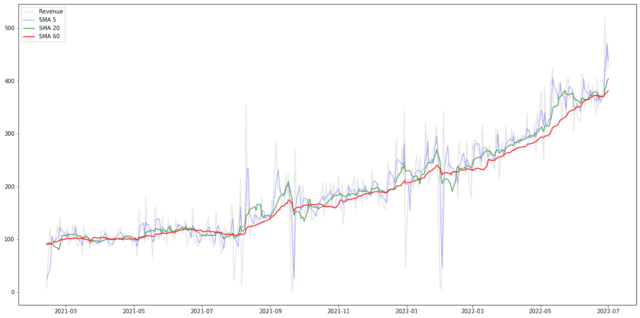
위 그래프를 보면, k 값이 증가함에 따라 그래프가 완만해지는 것을 확인할 수 있습니다. 즉, 불규칙한 변동분이 사라지고, 추세가 보다 명확하게 드러납니다. k 값은 적정 수준의 추세 패턴을 찾을 때까지 반복적인 시행착오 과정을 통해서 결정합니다.

계절성을 포함한 성분 분해

계절 성분은 어떤 단위 기간 내에서 순환하는 주기의 영향을 나타냅니다. 이름 처럼 봄, 여름, 가을, 겨울과 같은 계절의 영향뿐 아니라, 요일별 패턴, 국가별 휴일 또는 사업 휴무일의 영향, 경우에 따라서는 사업적인 특성(e.g. 매 월 또는 연 말 정기적으로 할인 행사를 진행하는 경우 =? 올리브영)도 계절성에 포함됩니다. 계절성을 내포하고 있는 데이터의 경우, 시계열 데이터는 처음 설명했던 것처럼 추세, 계절 그리고 두 가지 성분으로 설명되지 않는 불규칙 영향으로 분해할 수 있습니다.

성분 분해는 크게 덧셈(additive model; 가법 모델) 분해와 곱셈(multiplicative moel; 승법 모델) 분해 두 가지 방법으로 이루어집니다. 가법 모델은 시계열 데이터를 구성하는 각 성분이 덧셈을 통해 연결되어 있다고 가정하고, 승법 모델은 각 성분이 곱셈을 통해 연결되어 있다고 가정합니다. 이 때, 승법 모델은 로그 변환을 통해 가법 모델로 쉽게 변환 할 수 있어요.

• Additive model : y(t) = Trend + Seasonality + Noise
• Multiplicative model : y(t) = Trend x Seasonality x Noise

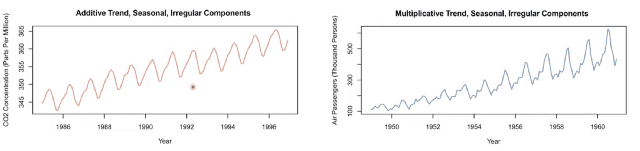
모델 선택은 시계열 데이터의 특성을 고려하면 되는데, 아래 그림의 왼편 그래프와 같이 시간에 따른 데이터 변동이 일정한 경우는 가법 모델을 활용한 데이터 분해가 적합합니다. 반대로, 변동폭이 관측값의 수준에 비례해서 변하는 경우 승법 모델을 적용하는 것이 좋습니다.

가법 모델을 기초로 기본 원리를 설명 해보겠습니다.

• 앞서 이동 평균을 구할 때 사용한 k 값을 데이터의 주기에 맞게 설정합니다. 일반적으로분기 데이터인 경우 k=4, 월별 데이터의 경우 k=12, 주별 규칙을 가지고 있는 일 데이터에서는 k=7로 설정합니다. 이렇게 설정한 값을 기초로 추세 성분을 계산합니다. 위에서 함께 확인한 그래프와 같이 평활(smoothing)된 추세를 확인할 수 있어요.
• 실제 관측값에서 추세를 제거한 시계열을 계산합니다. (y(t) - Trend)
• 계절성분을 측정하기 위해, 계절별 추세를 제거한 값(y(t) - Trend)의 평균을 구합니다. 이렇게 하면 계절 성분 값이 0 근처의 값이 되도록 조정되는데, 이때 계절별 값을 순서대로 모으고 각 연도의 데이터에 대한 수열을 복제해서 계절 성분을 구해 Seasonality 값을 얻을 수 있습니다.
• 마지막으로 관측값에서 계절성과 추세 성분을 빼서 나머지 불규칙 성분을 계산합니다. (Noise = y(t) - Trend - Seasonality)

Python의 statsmodels 패키지의 seasonal_decompose() 함수를 활용하면 간단하게 시계열 성분을 분해할 수 있습니다. 제가 구상한 데이터는 주말을 제외한 월-금요일에만 관측값이 존재하기 때문에, 한 달 주기로 계절성 확인을 위해 freq=20으로 설정했습니다.

코드를 실행하면 아래와 같은 결과를 얻을 수 있습니다. 전반적으로 우상향 하는 Trend를 확인할 수 있고, Seasonal 성분은 20일을 주기로 반복됩니다. 그리고 Trend + Seasonal 값과 Observed 값의 차이가 Residual로 나타납니다.

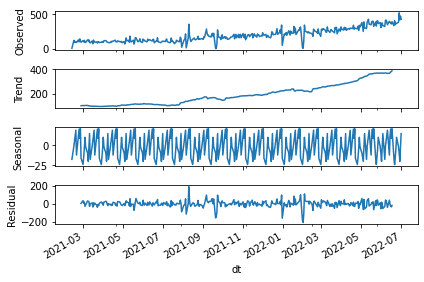
이번 글에서는 성분 분해의 원리를 쉽게 설명하기 위해 고전적인 분해 방식을 사용했는데요. 실제 시계열 분석을 진행할 때 추천되는 방법은 아닙니다. statsmodels.tsa.seasonal 패키지 Source에 조차 “This is a naive decomposition. More sophisticated methods should be preferred.”라는 문구가 적혀있어요. 대안으로 STL(Seasonal and Trend decomposition using Loess), SEASTS(Seasonal Extraction in ARIMA Time Series) 등을 활용할 수 있지만, 이번 글에서 자세히 다루지는 않겠습니다.

다만, 고전적인 분해 방식이 가지는 문제점에 대해서는 간단히 짚어보도록 해요.

• 앞서 추세 꺼내보기 부분에서도 설명했지만, sesonal_compose()는 이동 평균을 활용하기 때문에 설정한 주기가 k일 때 데이터 양 끝의 (k-1)/2개 관측값에 대한 추세 추정 값을 얻을 수 없습니다.
• 계설 정분이 매년 반복된다고 가정합니다. sesonal_compose() 결과를 보면 Seasonal 값이 20일 주기로 완전히 동일하게 반복되는 것을 확인할 수 있는데요. 현실에서는 시간적인 변화에 따라 계절성 또한 달라지게 되지요.
• 특정 기간의 시계열 값이 크게 튈 수 있습니다. 위 분해 결과에서도 21년 8월 상반기, 21년 9월 하반기, 21년 연말, 22년 2월 초순 등 일부 구간의 잔차가 아주 크게 나타나는 것을 볼 수 있어요.

아직 시계열 분석을 통해 미래를 예측하기 위해서는 갈 길이 멀지만, 시계열을 구성하는 중요한 세 가지 성분에 대해서 알게 되었습니다. 다음 글에서는 시계열 분석을 정복하기 위해 꼭 이해해야 하는 몇 가지 기본 개념을 정리해 보겠습니다.

현생에 쉼 없이 치이겠지만, 빠른 시간 내에 새 글을 가지고 돌아올 수 있기를 빌어주세요. 곧 다시 만나요! 👋

Reference

• 곽기영. (2020, December 16). 통계데이터분석 - 시계열분석 - 시계열 데이터 분해. Youtube. youtu.be/cUS2uISiwCA. Accessed on 2022, July 9.
• Hyndman, R.J., & Athanasopoulos, G. (2018) Forecasting: principles and practice, 2nd edition, OTexts: Melbourne, Australia. OTexts.com/fpp2. Accessed on 2022, July 10.