• 본 글은 박지용 교수님의 Summer session material과 Reference 논문 내용을 중심으로 정리하고 저의 해석을 덧붙이는 방식으로 작성되었습니다.

1. Causal Discovery 개요

인과추론 개념을 살짝 맛보고 나니 이거 공부는 끝이 없겠구나 싶어 우선 실무에 적용해기로 합니다. 분석 계획을 세우고 시작해보려는 순간 이런 고민이 들었습니다 - Causal diagram은 어떻게 그려야 하지?

Causal diagram은 인과 구조를 어떻게 설계하느냐에 따라 Treatment 추정 효과가 달라질 수 있는 만큼 분석가가 Domain knowledge를 기반으로 잘 구성하는 것이 중요합니다. 또한 구조적 인과 모형(Structural Causal Model)을 사용하지 않더라도 공변량을 정의할 때 도움을 주는 과정이라고 생각합니다. 이처럼 분석의 뼈대가 되는 Causal diagram을 도메인 지식보다 좀 더 확실한 근거를 가지고 만들 수 있는 방법이 있을까요?

Causal Discovery는 관측 데이터로부터 인과구조를 추론하는 기법입니다. 큰 틀에서 인과추론 분석이 인과 그래프를 정의하고 이러한 인과구조의 가정 하에 관측 데이터를 분석하여 Treatment effect를 추정한다면 (Causal graph → Data), Causal discovery는 역으로 데이터를 가지고 그 안에 숨어있는 인과구조를 찾아내는 것이 목적입니다(Data → Causal graph)

이 과정은 마치 녹은 물에서 녹기 전의 얼음 모양을 추론한 것과 같습니다. 관측된 데이터에는 이미 인과구조의 영향력이 반영되어 있으니 데이터를 보고 원래의 인과구조를 추론합니다. 다만 관측된 데이터의 결과를 만들어낼 수 있는 모델은 다양할 수 있기 때문에 추론 과정이 쉽지는 않습니다.

2. Basic Assumptions for Causal Discovery

Causal discovery는 4개의 기본 가정을 전제로 합니다.

1. Acyclicity (비순환성)

• 변수 간의 관계가 한 방향으로 이어지지만 순환하지는 않는다. SCM은 기본적으로 DAG에 기반하기 때문에 Acyclicity를 전제로 합니다.

2. Markov property

• 모든 노드는 descendant 노드에만 dependent 하다. 즉, parent 노드를 conditioning하면 descendant 노드는 다른 변수들과는 independent 하게 됩니다.

  

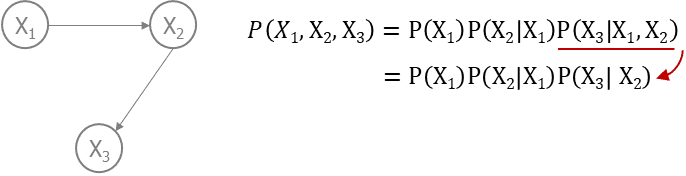
  그림으로 보면 X3는 X2와 dependent, X1과는 conditionally dependent한 관계이지만 parent node인 X2를 통제하게 되면 X1과는 independent하게 됩니다. 이러한 Causal markov assumption 덕분에 복잡한 joint distribution 수식을 단순하게 만들어 확률값 산출을 가능하게 합니다.

3. Faithfulness

• 인과 그래프 상에서 연결된 노드들은 반드시 확률적으로 dependent 하다.

  

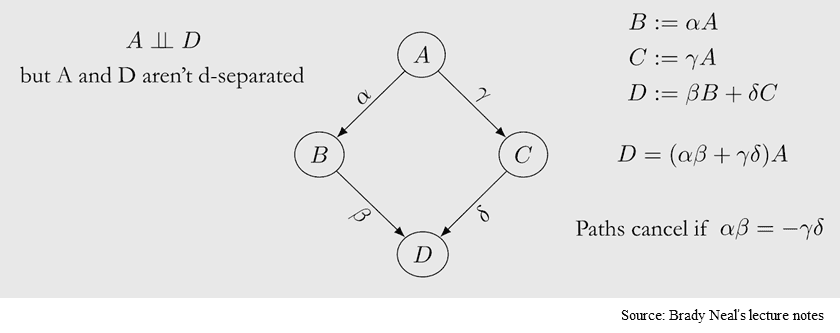
  인과 그래프에서 edge로 연결된 노드 간에 확률적 종속성이 있다는 말이 당연할 수도 있지만 위의 그림처럼 반례도 있습니다. A와 D는 실제로는 종속관계이지만 양방향의 path로 인해 각각의 인과효과가 상쇄되어 확률적으로는 독립적인 것처럼 보이게 됩니다. Faithfulness 가정은 이처럼 상쇄효과가 발생하는 경우는 없다고 보고, 확률적으로 독립적이라면 두 노드 간에는 연결성이 없다고 판단할 수 있습니다. (그림2)에서 X2를 통제할 때 X1과 X3가 independent하다면 X1과 X3 사이에는 어떠한 직접적인 연결성이 없다고 봅니다.

4. Sufficiency

• 인과 그래프 상에서의 노드 pair는 외부 요인에 영향을 받지 않는다. 그래프에 포함된 노드의 pair 만으로도 노드 간 관계에 대한 설명이 충분하다는 관점에서의 가정인 것 같습니다.

3. Method

우선 방법론에 대한 이야기를 하기 전에 Markov equivalence class(마코브 등가 클래스)에 대한 이해가 선행되어야 합니다. Markov equivalence class는 동일한 조건부 독립성을 표현하는 DAG의 그룹입니다.

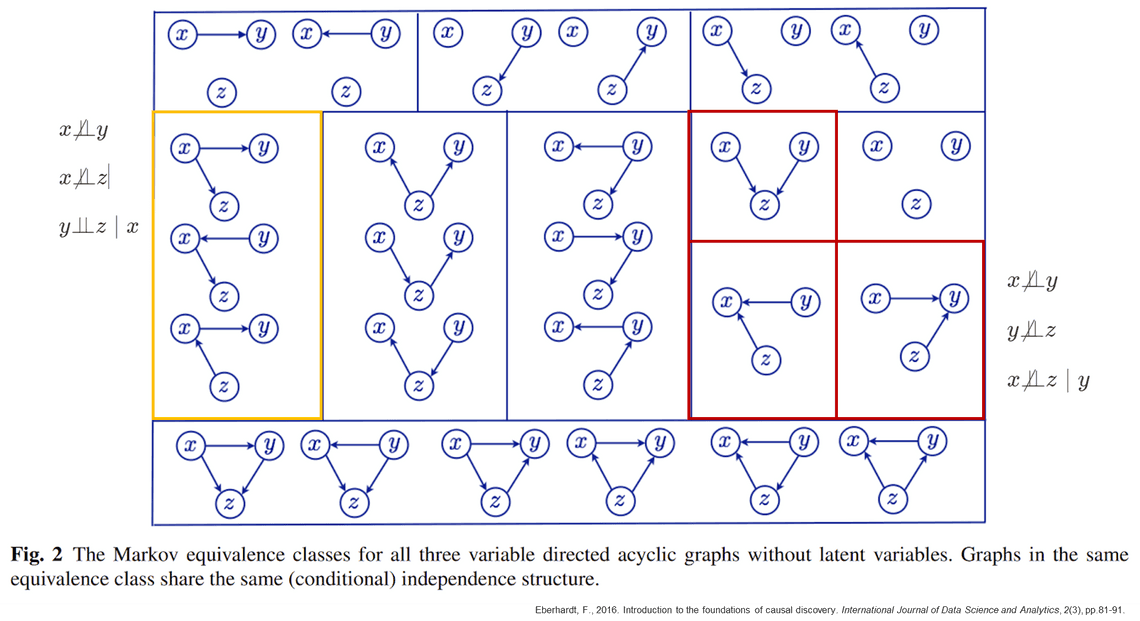
노란색 박스의 DAG 그룹은 x, y, z 3개 노드가 있을 때 (x,y), (x,z)는 종속적이고 x를 conditioning 할 때 y와 z가 독립이 되는 경우에 가능한 구조를 모두 표현한 것입니다. Causal discovery에서 핵심적으로 활용되는 부분은 빨간색 박스처럼 단 하나의 그래프 구조를 갖는 경우입니다. V-structure, 즉 collider가 발생하는 경우를 찾아 그래프의 구조를 확정지어 나가는 방식으로 전체 인과구조를 그리게 됩니다.

Causal discovery에서 아직 대표 방법론은 없지만 크게 3가지 관점으로 접근합니다.

1. Constraint-based

Constraint-based 방식은 conditional independence를 활용하는 방법론으로 잘 알려져있는 알고리즘으로는 PC과 FCI가 있습니다. PC와 FCI의 차이점은 PC는 unobserved confounder가 없다고 가정하고, FCI는 그 존재를 인정한다는 점입니다.

1-1. PC 알고리즘

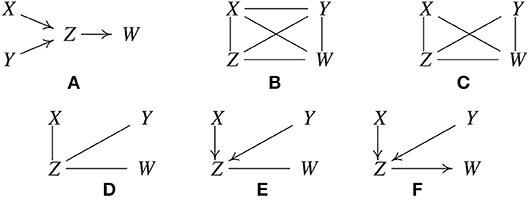
PC 알고리즘이 인과구조를 찾아가는 방식은 다음과 같습니다. A가 실제 인과관계라고 할 때,

1. 모든 노드(변수)를 연결하는 undirected graph를 구성합니다(B)

2. 변수를 통제하지 않은 상황에서도 독립적인 변수(unconditionally independent)들을 찾고, 그 변수 간의 edge를 지웁니다(C). 실제 인과 그래프를 보면 X와 Y는 unconditionally independent 하므로 X-Y간 edge를 제거 합니다.

3. 3개의 노드 간 관계에서 1개의 변수를 통제했을 때 나머지 두 변수가 independent 하다면(conditionally independent) 나머지 두 변수 간 edge를 지웁니다(D). 예를 들어 (X, W)에 대해 Z를 conditioning 했을 때, $X{\perp\!\!\!\perp}W\;|\;Z$ 라면 X와 W 간에는 Z를 통한 path 이외의 direct path는 없기 때문에 X-W 간 edge를 지울 수 있습니다.

4. 3번 단계를 conditioning variable의 수를 늘려가며 모든 케이스를 확인합니다. 4번 단계를 마치면 노드 간 유효한 edge만 남긴 구조를 얻게 되고, 이를 skeleton이라고 합니다.

5. Skeleton에서 V-structure 후보 중 발생 가능한 경우를 찾습니다(E).

   

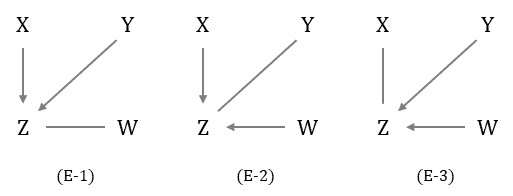
   E에서 발생할 수 있는 V-structure는 3가지인데 사실상 발생 가능한 케이스는 (E-1) 사례 뿐입니다. V-structure가 성립하려면 Z를 conditioning 했을 때 두 변수가 dependent 관계여야 하는데, 실제 인과관계를 보면 $X{\perp\!\!\!\perp}W\,|\,Z,\; Y{\perp\!\!\!\perp}W\,|\,Z,\; X{\not\perp\!\!\!\perp}Y\,|\,Z$ 이므로 (E-1)의 구조를 유효하다 볼 수 있습니다.

6. 나머지 edge의 방향이 collider 구조를 갖지 않는다면 방향을 결정해줍니다 (Orientation propagation). 이 단계에서 모든 edge가 방향성을 갖지 않은 상태로 도출될 수도 있습니다.

1-2. FCI 알고리즘

FCI 알고리즘은 skeleton을 도출하는 4단계까지의 프로세스는 PC와 동일하나 이후 단계에서 unobserved confounder의 존재를 가정하고 그래프를 탐색합니다.

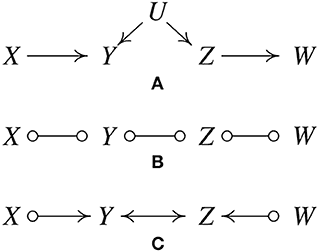
1. PC 알고리즘과 동일한 단계를 거쳐 skeleton을 도출합니다(B). FCI는 방향성에 대해 왼쪽, 오른쪽, 양방향 세 가지의 경우의 수를 고려하기 때문에 직선으로 정의하지 않고 동그라미로 표시합니다.
2. X-Y-Z 간의 관계를 살펴보면 X와 Z는 독립 관계인데 Y를 conditioning하면 dependent하게 된다는 점에서 Y가 collider임을 알 수 있고, 동일한 방식으로 Y-Z-W 관계에서 Z가 collider임을 확인하여 Y-Z 간에 latent confounder가 있음을 알려줍니다.

2. Score-based

Constraint-based 방식이 conditional independence를 가지고 edge를 제거해나가고 방향을 결정하는 방식이라면, Score-based 방식은 zero-base에서 edge로 연결된 노드를 추가해 나가면서 가장 최적화된 인과구조를 그려나가는 방식입니다. 각 단계마다 BIC score (Bayesian Information Criterion score)가 가장 최적화되는 방향으로 edge를 더하거나 제거하는 방식으로 최종적인 인과 그래프를 찾습니다.

대표적인 알고리즘은 GES(Greedy Equivalence Search)로 이 방법론 또한 unobserved confounder가 없다고 가정하고 Markov equivalence class를 output으로 제공합니다. GES와 FCI를 결합한 GFCI 모델은 GES로 skeleton을 그리고 edge의 방향성은 FCI로 찾는 방식으로 FCI 알고리즘보다는 성능이 좋은 것으로 알려져 있습니다.

3. Exploiting asymmetry (불균형성을 이용한 접근법)

세 번째 관점은 A→ B의 인과관계에서 A는 B에 영향을 줄 수 있지만, B가 A에는 영향을 줄 수 없다는 불균형성을 이용하여 인과관계를 찾는 방법입니다. 이 방법론 만으로 인과 그래프를 도출한다기 보다는 1, 2번째 관점을 검증/보완하는 방식으로 활용되는 것 같습니다.

• Time asymmetry: 원인이 발생한 후 결과가 발생한다는 시간의 차를 이용한 Granger causality. 인과 구조를 도출하기에는 부족하지만 원인과 결과의 방향성에 대한 정보를 제공합니다.
• Complexity asymmetry : 여러 개의 인과모델 후보가 있다면 가장 단순한 모델이 낫다는 이론으로 데이터 길이의 복잡성을 측정하는 Kolmogorov complexity로 판단합니다.
• Functional asymmetry : 후보 모델 중 인과관계에 대한 예측 정확도가 높은 모델을 고르는 방식으로 원인변수와 noise term 간의 independency를 판단하여 independent 한 경우 모델을 유효한 것으로 판단하는 NANM(Non-linear Additive Noise Model) 알고리즘 등이 있습니다.

4. 글을 마치며

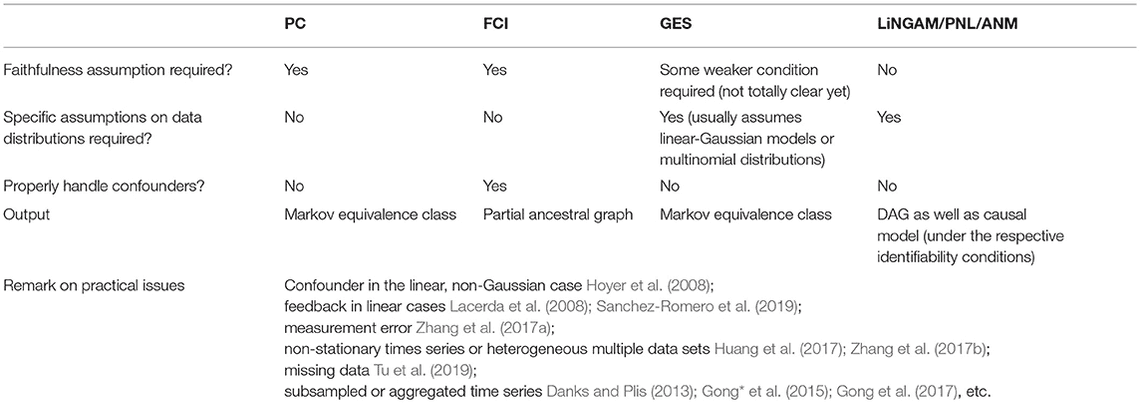
본 글에서 소개한 방법론 이외에도 많은 방법론들이 존재합니다. 그 중 특정 방법론이 가장 뛰어다다기 보다는 각각의 장단점이 있습니다.

PC와 FCI, GES 알고리즘은 conditional independence를 input으로 사용하기 때문에 linear model에는 적용이 어렵지 않으나 non-linear 모델에는 다소 복잡할 수 있습니다. 그래프 서칭에 있어 변수의 확장이 용이하나 Markov equivalence class를 output으로 제공하기 때문에 때로는 두루뭉술한 결과를 받아볼 수도 있습니다. 또한 구조방정식 기반의 방법론 자체가 인과 관계의 함수 형태에 영향을 많이 받기 때문에 latent confounder를 적절히 처리하기 어려울 수도 있습니다.

반면 non-Gaussian 또는 non-linear causal model은 인과 관계에 대해 보다 상세한 정보를 제공할 수는 있으나 변수의 확장성 측면에서는 한계가 있다고 합니다 (최근 모델은 변수 12개까지 커버).

따라서 방법론 선택 전에 변수의 distribution을 확인하고, 활용하고자 하는 변수의 개수 등을 고려할 필요가 있겠습니다. 본 글에 이어서 다음 회차에는 실 데이터로 3가지 방법론을 적용했을 때의 결과를 비교해보고, conditional independence test 방식에 대해 살펴보고자 합니다.

Reference

1. Clark Glymour, Kun Zhang and Peter Spirtes, 2019. Review of Causal Discovery Methods Based on Graphical Models. Frontiers in Genetics, 10, p.524
2. Korea Summer Session on Causal Inference 2021 [18-3]
3. https://towardsdatascience.com/causal-discovery-6858f9af6dcb