Table Of Contents
쓰는 용어
- AB Test : A와 B 대안이 있을 때 어떤 대안이 더 효과적인 지를 알아보기 위해 대상자를 임의로 절반으로 나누어 그 인과적 관계를 살펴보는 방법
- 전환율 (Conversion rate): A와 B 대안으로 인해 구매 혹은 다음 페이지로 전환되는 비율
- 클릭율 (CTR; Click-Through Rate): A와 B 대안으로 인해 클릭되는 비율
- 인과 관계 (Causal Relationship): 설명 변수가 원인, 반응 변수가 결과가 되어 그 원인으로 결과가 얼마나 바뀌는 지를 추정
- 무정보 사전분포 (Non-informative Prior) : 베이지안에서 쓰는 사전 분포 중 특정한 사전 지식이 없을 때 주는 사전 분포
- 켤레성 (Conjugacy) : 사전 분포와 사후 분포가 같은 분포인 경우 띠는 성질
- p-value : 귀무 가설이 맞다는 전제 하에, 표본에서 실제로 관측된 통계치와 같거나 더 극단적인 통계치가 관측될 확률
A/B 테스트란?

출처: https://www.optimizely.com/ab-testing/
권정민님의 실무에서 활용하는 AB 테스트 발표자료에 따르면 AB Test은 사용자를 대상으로 한 실제 환경에서의 실험으로, A와 B��에 따라 관심 있는 지표가 어떻게 바뀌는 지를 판단하는 방법입니다. 여기서 관심있는 지표란 양적으로 확인할 수 있는 지표들로, 클릭율 (CTR), 전환율 (Conversion Rate) 등이 있습니다. 위 그림에서 예를 들면 A와 B 디자인의 광고 중 B 광고의 클릭율이 높기 때문에 B 디자인이 더 효과적이다 예상할 수 있죠.
그럼 A보다 B가 낫다고 말하기 위해서는 얼마나 더 지표들의 값이 높아야할까요? 이를 판단하기 위해 고안된 방법이 바로 AB Test입니다. 그러나, 실제 환경은 실험 환경처럼 관심 밖의 요인들을 완벽히 통제할 수 없습니다. 다른 요인들이 A와 B로 인한 효과를 방해하거나 촉진해서 인과 관계를 정확히 추정하기 어렵기 때문입니다.
그 대안으로 AB test에서는 A와 B 디자인에 노출되는 사람들을 무작위로 나누어 최대한 실험 환경과 비슷하도록 유사 실험 환경을 구축합니다. 이를 위해 AB Test 설계 과정은 다음과 같습니다.
- 사용자 및 지표 선정
- 실제 환경 선정
- 사용자 무작위 선정
- 사용자에게 무작위로 A와 B 노출
- 결과 분석 및 검증
전환율 검정 (Conversion Testing)
어떤 웹사이트에서 A와 B 디자인 중 어느 쪽이 구매로 전환되는 비율이 높은지 알아본다고 가정합시다. 즉, 웹사이트에 방문한 사람들이 A와 B 디자인 중 어느 디자인에 더 현혹되어 구매하게 되는 지를 알아보는 것이죠. 이를 위해 방문자에게 랜덤하게 A와 B 디자인 중 하나를 보여주고 구매 여부를 체크합니다. 이러한 과정을 Conversion Testing이라 합니다. 여기서 가설은 “A보다 B가 구매로의 전환율이 높을 것이다”와 같은 내용이 됩니다.
선택지가 A와 B로 2개이면 베이지안 AB test는 가능도 (Likelihood)로 이항 분포 (Binomial Distribution)를, 사전 분포 (Prior)로 베타분포 (Beta Distribution)를 선정합니다. 그 이유는 무엇일까요?
가능도: 이항 분포
가능도는 우리가 관측하는 데이터의 함수를 의미합니다. 우리가 관측하는 데이터는 각 방문자마다 A나 B를 통해 구매를 했는 지의 여부입니다.
이항 분포를 따르는 확률 변수는 명의 사람 중 어떤 event를 성공한 사람 수를 의미하기 때문에 우리의 데이터도 이항 분포를 따른다 가정할 수 있습니다. n명의 사람 중 성공한 사람 수를 X라 하고 그 성공 확률을 p라 할 때, 이항 분포는 다음과 같이 정의됩니다.
예를 들어, A디자인을 본 방문자는 1,300명이고 그 중 120명이 구매를 했고, B디자인을 본 방문자는 1,270명이고 그 중 125명이 구매했다 상상해봅시다. 이 때 구매 행위가 어떤 event를 성공했다 보고 각 사람들의 구매 행위가 독립적이라고 가정하면, A디자인을 보고 구매한 사람 수와 B 디자인을 보고 구매한 사람 수는 각각 이항 분포를 따릅니다.
여기서 는 각 A, B 디자인을 통해 구매로 전환한 확률인 전환율로, 이항 분포의 관심사인 모수 (parameter)입니다.
사전 분포: 베타 분포
베이지안은 모수에 사전 분포를 가정해 모수의 실제 값이 하나가 아니라, 사람들의 믿음 (belief)에 따라 달라지는 분포 형태를 띠고 있다 생각합니다. 여기서 관심 모수는 인 전환율이기 때문에 이에 잘 맞는 사전 분포를 가정하는 것이 중요합니다.
이를 위해 사전 분포로 베타 분포 (Beta Distribution)을 가정합니다. 베타 분포를 따르는 확률 변수는 항상 사이의 값이기 때문에, 성공 확률의 분포의 자연스러운 가정이 됩니다. 베타 분포는 다음과 같이 정의됩니다.
베타 분포의 모수인 의 값에 따라 확률이 ‘어느 값에 밀집되어 있을 것이다’에 대한 사전적인 지식을 부여할 수 있습니다. 예를 들어, 아래의 그림 중 주황색 선인 Beta(2,8)의 경우 p=0.12부근에서 확률밀도함수가 가장 높기 때문에 전환율이 0.12 부근이라는 배경 지식이 있다면 Beta(2,8)를 사전 분포로 사용할 수 있을 것입니다.
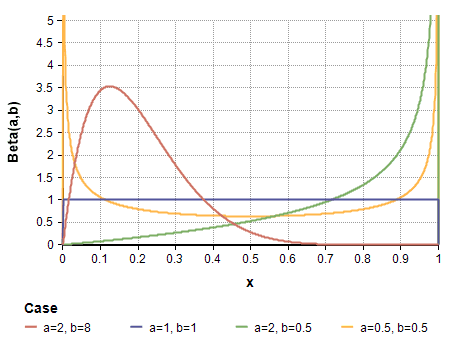
그러나, 특별한 사전 지식이 없을 경우 무정보 사전 분포 (Non-informative prior)를 주는 것이 일반적입니다. 무정보 사전 분포는 말 그대로 정보가 없는 사전 분포로, 베타 분포의 경우 Beta(1,1)에 해당합니다. Beta(1,1)을 구하면 로, 균등 분포인 Uniform(0,1)과 같습니다. 즉, 전환율에 대한 어떠한 지식도 없다면 전환율이 “(0,1) 사이 어딘가에 랜덤하게 있을 것이다”는 정보 없는 내용을 사전 분포로 가정할 수 있는 것입니다.
이러한 무정보 사전 분포를 쓰는 경우는
- 전환율에 대해 사전 지식이 없을 경우
- Frequentist가 추정하는 값과 같은 결과를 내고 싶을 경우, 즉 데이터만으로 모수를 추정하고 싶을 경우
로 생각보다 많이 쓰입니다. 저희도 A와 B 디자인의 전환율에 대한 사전 지식이 없다 가정하고 Beta(1,1)을 사전 분포로 사용하겠습니다.
사후 분포: 베타 분포
이제 A, B 방법의 전환율을 구하는 데 있어서 사전 분포는 베타 분포, 가능도는 이항 분포로 두는 것에 대해 자연스러우셔야 합니다. 사전 분포와 가능도를 각각 베타와 이항분포로 설정하는 것의 또 하나의 장점은 켤레성(Conjugacy)를 이용할 수 있다는 점입니다. 사후 분포(Posterior Distribution)를 구했을 때, 그 형태가 사전 분포와 같은 분포일 때 켤레성을 띤다고 말합니다.
사후 분포를 구하기 위해선 고등학교 때 배운 조건부 정�리를 이용합니다. 모수인 p와 관련있는 항만 남기고 정리하면 결국 사후 분포는 (가능도) (사전 분포)에 비례합니다.
따라서, 가능도가 이항 분포 Binomial(n,p)고 사전 분포가 Beta()일 경우,
아래 수식과 같이 사후 분포는 Beta(+x, +n-x)를 따르게 됩니다. 즉, 사후 분포의 첫번째 모수는 +성공 횟수(x), 두번째 모수는 + 실패 횟수 (n-x)가 됩니다.
따라서 무정보 사전 분포인 Beta(1,1)를 가정했을 때,
- A 디자인에 따른 전환율의 사후 분포는 Beta(1+120, 1+1300-120) = Beta(121, 1181),
- B 디자인에 따른 전환율의 사후 분포는 Beta(1+125, 1+1275-125)=Beta(126,1151) 를 따릅니다.
사후 분포에서 난수를 생성한 후 평균을 구하면 각 전환율의 추정치를 구할 수 있습니다. 이를 파이썬으로 구현하면 다음과 같습니다.
from IPython.core.pylabtools import figsizefrom matplotlib import pyplot as pltfrom scipy import stats as stimport numpy as npvisit_A = 1300visit_B = 1275conversion_A = 120conversion_B = 125alpha = 1beta = 1n_samples = 1000print(alpha)posterior_A = st.beta(alpha+conversion_A,beta+visit_A-conversion_A)posterior_B = st.beta(alpha+conversion_B,beta+visit_B-conversion_B)posterior_samples_A = st.beta(alpha+conversion_A,beta+visit_A-conversion_A).rvs(n_samples)posterior_samples_B = st.beta(alpha+conversion_B,beta+visit_B-conversion_B).rvs(n_samples)# posterior meanprint((posterior_samples_A > posterior_samples_B).mean())[Output] 0.31355
결과값인 0.31355은 A 디자인의 전환율이 B 디자인의 전환율보다 높을 확률이 31.36%정도밖에 되지 않음을 의미합니다. 다시 말하면, B 디자인 전환율이 A의 전환율보다 높을 확률이 68.64%이죠.
A 디자인의 전환율과 B 디자인의 전환율의 사후분포는 다음과 같이 그릴 수 있습니다. 오른쪽 그림은 단순히 왼�쪽 그림을 확대한 그림입니다.
# Posterior Dist of A and Bfig,axes = plt.subplots(1,2,figsize=(10,4))x = np.linspace(0,1,1000)i=0for ax in axes:ax.plot(x, posterior_A.pdf(x), label = "posterior of A: Beta(121,1181)")ax.plot(x, posterior_B.pdf(x), label = "posterior of B: Beta(126,1151)")ax.set_xlabel("Value")ax.set_ylabel("Density")if i==1:ax.set_xlim(0.05, 0.15)i+=1axes[0].legend()
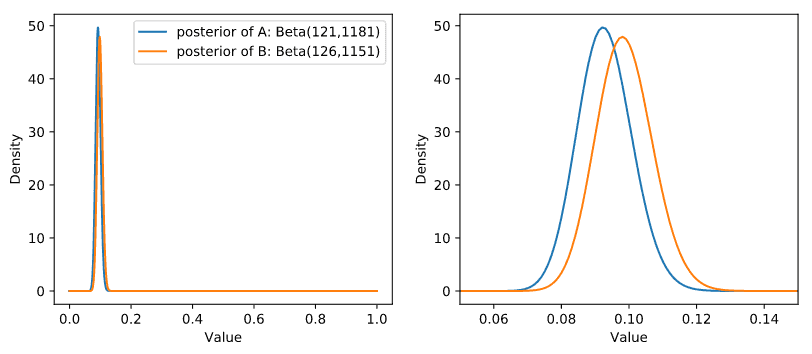
그림에서 보듯이, B 디자인의 전환율의 사후분포가 A보다 오른쪽에 위치함을 알 수 있습니다. 이렇게 앞에서 B 디자인 전환율이 A의 전환율보다 높을 확률이 68.64%인 것을 그림으로 확인해보았습니다.
기대 수익 분석 (Expected Revenue Analysis)
AB test를 더 자세하게 알아보기 전 기대 수익 (Expected Revenue)을 베이지안 관점에서 보는 방법에 대해 알아봅시다. 만약 어떤 웹사이트의 기대 수익이
로 정의가 되고, 은 각각 $79, $49, $25 가격 플랜을 선택할 확률이고 는 아무 플랜을 선택하지 않을 확률이라 가정합시다. 이 확률들은 더하면 1이 된다는 제약조건을 가지고 있습니�다.
이 때의 가능도 함수, 사전 분포는 어떻게 될까요? 정답은 이항 분포와 베타 분포의 확장판인 다항 분포 (Multinomial Distribution)와 디리클레 분포 (Dirichlet Distribution)입니다.
가능도: 다항 분포
만약 n명의 사람이 $79, $49, $25 가격 플랜 중 하나를 선택할 때 각 플랜 별 사람수를 라 하고 선택하지 않은 사람 수를 라 하면 가능도는 다항 분포를 따르고 다음과 같이 주어집니다.
사전 분포: 디리클레 분포
디리클레 분포는 베타 분포의 확장판으로 다음과 같이 모수 를 가집니다.
베타 분포와 마찬가지로 Dirichlet(1,1,1,1)도 무정보 사전 분포입니다.
사후 분포: 디리클레 분포
사전 분포로 Dirichlet(1,1,1,1)을, 가능도로 를 관측한 다항 분포를 따른다할 때, 사후 분포는 켤레성으로 인해 다시 디리클레 분포인 Dirichlet(1+, 1+,1+,1+)를 따릅니다.
Expected Revenue Analysis + AB Test
이제 앞에서 배운 내용들을 합쳐봅시다. A 디자인과 B 디자인이 있고, 이 디자인에 따른 기대 수익에 관심이 있습니다. 가격 플랜은 마찬가지로 월 $79, $49, $25의 세 개의 플랜이 있다 가정합시다. 관측된 데이터는 다음과 같습니다.
| 디자인 | 총 사람 수 | $79 선택 | $49 선택 | $25 선택 | 선택 X |
|---|---|---|---|---|---|
| A | 1000 | 10 | 49 | 80 | 864 |
| B | 2000 | 45 | 84 | 200 | 1671 |
| 합계 | 3000 | 55 | 133 | 280 | 2535 |
우리의 관심사는
- A와 B 중 어떤 디자인이 기대 수익을 더 많이 가져오는 지
- 기대 수익이 얼마나 더 많은 지
입니다.
Q1. A와 B 중 어떤 디자인이 기대 수익이 많을까?
이제 A 디자인과 B 디자인을 통해 $79, $49, $25의 세 가격 플랜을 선택하거나 아무 플랜도 선택하지 않을 확률에 디리클레 사전 분포를 가정합니다. 이 확률에 대해 사전 지식이 없으므로 두 디자인의 확률들의 분포 모두 Dirichlet(1,1,1,1)로 가정합니다.
또한, A 디자인과 B 디자인의 가격 플랜 별 사람 수는 다항 분포의 가능도를 가지게 됩니다. 위의 표와 비교했을 때 A 디자인에 노출된 사람수는 =1000, A 디자인에 노출된 사람 중 $75, $49, $25 가격 플랜을 선택한 사람 수를 각각 , 아무 플랜도 선택하지 않은 사람 수를 입니다. 또한 B 디자인도 마찬가지로 라 둘 수 있습니다.
따라서, A 디자인과 B 디자인의 선택지별 확률의 사후 분포도 켤레성에 의해 디리클레 분포를 따릅니다.
- A 디자인: Dirichlet() = Dirichlet(11,50,81,865)
- B 디자인: () = Dirichlet(45,84,200,1671)을 따르게 됩니다.
이를 파이썬으로 구현하면 p_A와 p_B가 바로 사후 분포의 랜덤 샘플이 됩니다.
n_A = 1000x1_A= 10x2_A= 46x3_A= 80x4_A=n_A-x1_A-x2_A-x3_An_B = 2000x1_B= 45x2_B= 84x3_B= 200x4_B=n_B-x1_B-x2_B-x3_Balpha_A=np.array([1+x1_A,1+x2_A,1+x3_A,1+x4_A])alpha_B=np.array([1+x1_B,1+x2_B,1+x3_B,1+x4_B])p_A = st.dirichlet(alpha_A).rvs(n_samples)p_B = st.dirichlet(alpha_B).rvs(n_samples)
하지만 저희의 관심사는 기대 수익입니다. 기대 수익은 앞에서 구한 것처럼 expected_revenue함수를 통해 기대 수익의 사후 분포를 구할 수 있습니다.
A 디자인과 B 디자인에 따른 기대 수익 사후 분포의 랜덤 샘플은 ER_A와 ER_B에 저장됩니다.
ER_A=expected_revenue(p_A)ER_B=expected_revenue(p_B)
이 사후 분포는 특정한 분포를 따르지는 않지만, 랜덤 샘플들이 어떻��게 분포되어 있는 지 히스토그램으로 확인할 수 있습니다.
plt.hist(ER_A,label="E[R] of A",bins=50,histtype="stepfilled",alpha=.8)plt.hist(ER_B,label="E[R] of B",bins=50,histtype="stepfilled",alpha=.8)plt.xlabel("Value"); plt.ylabel("Density")plt.legend(loc="best")
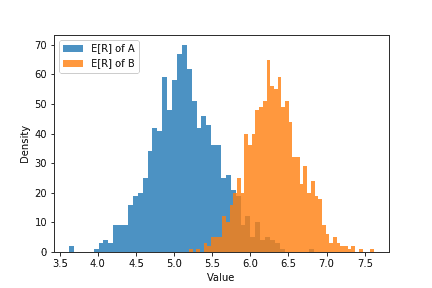
이 히스토그램을 보면 B 디자인의 기대 수익 분포가 A 디자인의 기대 수익 분포 보다 오른쪽에 위치합니다. 즉, B 디자인이 A 디자인보다 더 많은 기대 수익을 낼 것이라 예상할 수 있습니다.
그럼 B 디자인의 기대 수익이 A 디자인의 기대 수익보다 높을 확률은 얼마나 될까요? 아래의 코드처럼 계산하면 그 값은 0.981로 매우 높은 확률을 보입니다.
print((ER_B>ER_A).mean())[Output] 0.981
Q2. 기대 수익이 얼마나 더 많을까?
B 디자인의 기대 수익이 A 디자인보다 얼마나 더 많은 지 확인하는 방법은 이 두 기대수익의 차 (difference)의 사후 분포를 보는 것입니다.
plt.hist(ER_B-ER_A,histtype="stepfilled",color="red",alpha=0.5,bins=50)plt.vlines(0,0,70,linestyle='solid')plt.xlabel("Value")plt.ylabel("Density")plt.ylim(0,70)plt.title("Posterior Distribution of Difference of E[$R_B$]-E[$R_A$]")
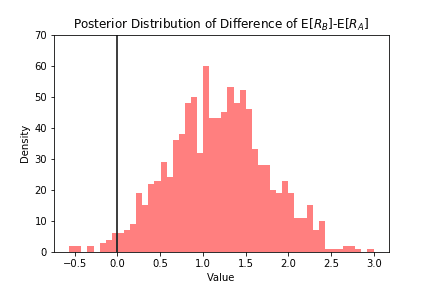
위의 그림을 보면 기대 수익의 차가 대부분 양수임을 볼 수 있습니다. 이의 점 추정치는 1.168이 됩니다.
print((ER_B-ER_A).mean().round(3)) #1.168
Frequentist vs. Bayesian t-test
t-test는 전통적인 빈도론적인(Frequentist) 가설 검정 방법으로 정해진 값에서 얼마나 표본 평균 (Sample Average)이 벗어나 있는 지를 봅니다. 이를 AB test에 적용하면 2표본-가설검정입니다. 앞에서 다룬 AB test와 달리 이 검정의 주체는 연속된 시간으로 연속형이기 때문에 t-test를 사용합니다.
John K. Kruschke는 이를 베이지안 버전으로 확장해 BEST (Bayesian Estimation Supersedes t-test)를 고안했습니다. 기존의 t-test과의 차이점은 다음과 같습니다.
| 질문 | Frequentist | Bayesian |
|---|---|---|
| 이상치가 포함되어도 괜찮은가? | No | Yes |
| 가설검정을 어떻게 하는가? | p-value 기반 | HDI 기반 |
Q1. 이상치가 포함되어도 괜찮은가?
자료에 이상치가 포함되어도 괜찮은가의 여부는 가설 검정을 하기 전 데이터의 분포를 어떤 것으로 가정하느냐에 따라 다릅니다. Frequentist t-test는 데이터가 정규 분포를 따른다 가정하지만, Bayesian은 데이터가 t 분포를 따른다 가정합니다.
정규 분포와 t 분포의 차이는 tail의 두께입니다. 정규분포에 비��해 t 분포는 heavy tail이고 자유도 가 커질수록 정규분포에 근사합니다. heavy tail이라는 말은 데이터의 분산이 큼을 의미하고, 그만큼 이상치를 포함한다 말할 수 있습니다.
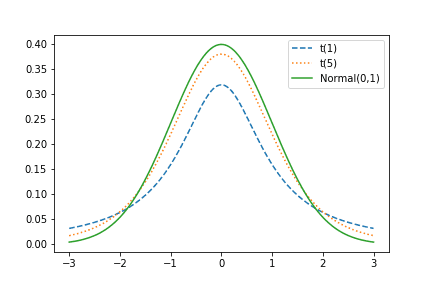
Frequentist t-test는 A와 B 방법에 각각 노출된 두 표본 집단이 정규 분포를 따른다 가정하고, 표본 평균과 표본 분산을 통해 t 통계량 ()를 산출합니다. 만약 데이터가 정규분포를 따르지 않을 경우 이상치를 제거하여 보정합니다.
이에 비해, BEST는 데이터가 t 분포를 따른다 가정하고 이상치가 있어도 분포 가정을 위배하지 않기 때문에 가설 검정 결과를 신뢰할 수 있습니다.
Q2. 가설 검정을 어떻게 하는가?
p-value 는 귀무 가설이 맞다는 전제 하에, 표본에서 실제로 관측된 통계치와 ’같거나 더 극단적인’ 통계치가 관측될 확률입니다. 만약 귀무가설이 “A와 B 간의 CTR 차이가 없다”라면, 실제로 관측된 CTR 차이에 대한 통계치 ()를 구해 귀무가설 하의 t 분포 () 내에서 와 같거나 더 극단적인 통계치가 관측될 확률 이 p-value가 됩니다.
Frequentist는 이 p-value가 유의 수준 (보통 0.05)보다 작을 때 귀무 가설을 기각합니다. 그러나 이 p-value는 표본 크기에 따라 바뀌는 문제가 있습니다. A와 B디자인의 CTR이 차이를 보여도 표본 크기가 커지면 p-value도 작아져 가설을 기각하는 경우가 많아지게 되는 것이죠. 이에 대한 자세한 예시는 박�장시님의 AB 테스트에서 p-value에 휘둘리지 않기에서 확인하실 수 있습니다.
이에 비해 BEST는 p-value 대신 HDI (Highest Density Interval)을 이용합니다. HDI란 분포에서 가장 높은 확률 밀도를 나타내는 범위를 의미하고, 이 범위 안에 있는 값들은 가장 신뢰할만한 (credible) 값들입니다. 아래의 그림처럼, 분포에서 95% HDI에 속한 값들은 분포의 95%를 커버하고, 가장 높은 확률을 보이는 값들로 구성되어 있습니다.
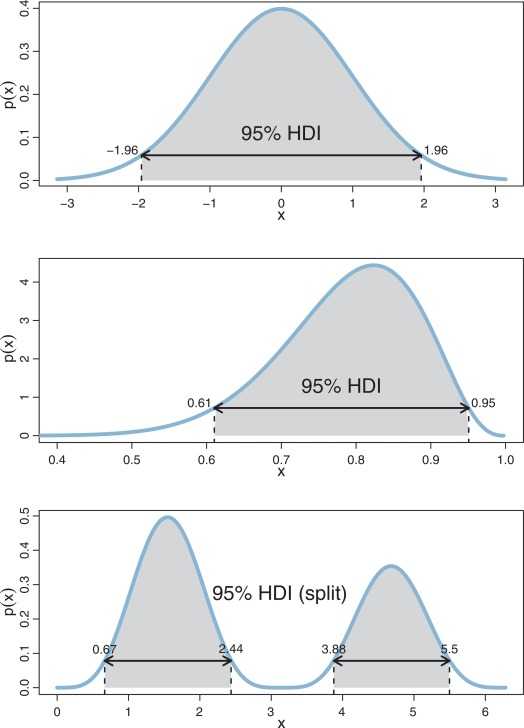
HDI는 Frequentist의 신뢰 구간 (Confidence Interval)과 비슷하지만 해석 상 더 직관적입니다. “95%의 확률로 모수가 이 구간 안에 있다”는 걸 말할 수 있는 건 HDI뿐입니다. Frequentist의 95% 신뢰 구간은 무한 번 표본 추출할 때마다 구한 신뢰구간 중 95%이 참값인 모수를 포함함을 의미합니다. 만약 100번의 표본을 추출했다면 그 각각의 신뢰구간 중 95개가 참값을 포함한다는 것이죠. 그러나 사실상 무한 번 표본을 추출하는 것이 불가능하니 이는 가상적인 내용이고 이론 상 존재하는 내용입니다. 따라서 HDI가 만약 0을 포함하고 있는 구간이라면 가설 검정 결과는 귀무 가설을 지지할 것이고, 포함하지 않는다면 대립 가설을 지지하게 됩니다.
BEST Procedure for AB Test
A와 B 디자인에 따른 웹사이트 이용 시간의 차이를 BEST로 검정해봅시다. 이를 위해 각각 250명씩 A와 B 디자인에 노출되었다 가정했습니다. A 디자인을 쓴 웹사이트의 이용시간은 평균이 30이고 표준편차가 4인 정규분포를 따르고, B 디자인을 쓴 웹사이트의 이용시간은 평균이 26, 표준편차가 7인 정규분포를 따르도록 데이터를 생성했습니다.
import numpy as npimport matplotlib.pyplot as pltimport pymc as pmN=250mu_A, std_A = 30,4mu_B, std_B = 26,7duration_A = np.random.normal(mu_A,std_A,size=N)duration_B = np.random.normal(mu_B,std_B,size=N)print (duration_B[:8])
[22.07725479 36.92520693 18.43953839 43.34529828 22.12233658 29.4195634324.81570352 16.88348905]
B의 이용시간을 보면 편차가 꽤 큼을 확인할 수 있습니다. 그렇기 때문에 t 분포로 가정하는 것이 좀 더 강건한 결과를 낼 수 있습니다.
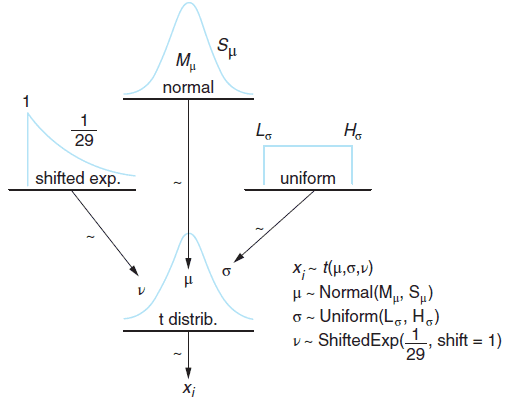
BEST 모형의 Graphical Representation. (출처: Bayesian Methods for Hackers)
위의 그림에서 보듯이 BEST모형의 데이터에 해당하는 가 평균 와 표준편차 , 자유도가 인 t 분포 가능도를 가진다 가정합니다. 이를 위해 에 사전 분포를 다음과 같이 정의합니다.
사전 분포
, 사전 분포: 정규 분포
- 평균: A 이용 시간과 B 이용 시간의 합동 평균 (pooled mean)
- 표준 편차: A 이용 시간과 B 이용 시간의 합동 표준 편차 (pooled standard deviation)$\times$1000
pooled_mean = np.r_[duration_A,duration_B].mean()pooled_std = np.r_[duration_A,duration_B].std()tau = 1/(1000*pooled_std**2) # precision parameter# Prior on mu_A and mu_Bmu_A = pm.Normal("mu_A",pooled_mean,tau)mu_B = pm.Normal("mu_B",pooled_mean,tau)np.r_를 통해duration_A와duration_B를 한 array로 만들어서 합동 평균과 합동 표준편차를 구합니다.tau는 정밀도 모수 (precision parameter)로 1/분산으로 정의됩니다.pymc에서Normal에 들어가는 모수가 평균과 정밀도이기 때문에tau를 생성하였습니다.또한 에 대한 사전 지식이 없기 때문에 무정보 사전 분포를 정의하는 것이 좋습니다. 이를 위해 정규 분포의 표준편차에 1000을 곱하여 분산을 크게 합니다. 따라서,
tau에1/pooled_std**2대신1/(1000*pooled_std**2)로 씁니다.사전 분포: 균등 분포
하한 (Lower bound): 합동 표준 편차/1000
상한 (Upper bound): 합동 표준 편차*1000
std_A = pm.Uniform("std_A", pooled_std/1000, 1000*pooled_std)std_B = pm.Uniform("std_B", pooled_std/1000, 1000*pooled_std)마찬가지로, 하한과 상한의 범위를 매우 크게 해서 무정보 사전 분포로 정의합니다. 이 때 주의할 점은 표준편차는 항상 양수이기 때문에 음수 값이 나오지 않도록 사전 분포를 정의해주어야 한다는 점입니다.
- 자유도 의 분포: 이동된 지수 분포 (Shifted Exponential)
nu_minus_1 = pm.Exponential("nu-1",1/29)
여기서 자유도는 항상 1 이상이니 이동된 지수 분포를 이용해�서 최소값이 0이 아닌 1이 되도록 정의하지 않았나 싶습니다..!
가능도: 비중심 t-분포 (Noncentral t-distribution)
가능도는 앞서 말씀드린 것처럼 t 분포를 사용합니다. 보통의 t 분포는 자유도 모수 만 고려하면 되지만 비중심 t-분포는 자유도 모수 외에도 location 모수 와 scale 모수 를 가집니다. p.d.f는 다음과 같이 정의됩니다.
obs_A = pm.NoncentralT("obs_A",mu_A, 1/std_A**2, nu_minus_1+1, observed=True, value = duration_A)obs_B = pm.NoncentralT("obs_B",mu_B, 1/std_B**2, nu_minus_1+1, observed=True, value = duration_B)
위 코드는 데이터인 duration_A가 duration_B가 비중심 t-분포를 따름을 보여주는 코드입니다.
MCMC
이제 사후 분포를 구하기 위해 MCMC sample을 생성합니다. 앞의 예제와 달리 사후 분포가 알려진 형태가 아니지만, pymc를 통해 가능도와 사전 분포만 정의해줘도 사후 분포의 sample을 추출할 수 있습니다.
mcmc = pm.MCMC([obs_A,obs_B,mu_A,mu_B,std_A,std_B,nu_minus_1])mcmc.sample(iter=25000,burn=10000)mu_A_trace = mcmc.trace("mu_A")[:]mu_B_trace = mcmc.trace("mu_B")[:]std_A_trace = mcmc.trace("std_A")[:]std_B_trace = mcmc.trace("std_B")[:] #[:]: trace object => ndarraynu_trace = mcmc.trace("nu-1")[:]+1
sample()의 인자는 iter, burn, thin으로 iter는 전체 MCMC를 돌리는 횟수, burn은 MCMC 초기 sample 중 버리는 갯수, thin은 MCMC sample을 추출하는 간격을 의미합니다.
만약 iter=a, burn=b, thin=c로 설정되어 있다면, 우리가 최종적으로 갖는 사후 분포 sample의 개수는 (a-b)/c입니다!
우리의 경우 25,000 sample 중 10,000개의 초기 sample을 버리고 매 sample을 추출하도록 세팅해 모수마다 15,000개의 sample을 가집니다.
trace()는 최종 MCMC sample들을 출력하는 함수입니다. [:]는 객체를 trace에서 ndarray로 바꿔주기 위��한 작업입니다.
결과 해석
각 모수들의 사후 분포 sample을 히스토그램으로 그리면 다음과 같습니다.
def _hist(data,label,**kwargs):return plt.hist(data,bins=40,histtype="stepfilled",alpha=.95,label=label, **kwargs)ax = plt.subplot(3,1,1)_hist(mu_A_trace,"A")_hist(mu_B_trace,"B")plt.legend ()plt.title("Posterior distributions of $\mu$")ax=plt.subplot (3,1,2)_hist(std_A_trace,"A")_hist(std_B_trace,"B")plt.legend ()plt.title("Posterior distributions of $\sigma$")ax=plt.subplot (3,1,3)_hist(nu_trace,"",color="#7A68A6")plt.title(r"Posterior distributions of $\nu$")plt.xlabel("Value")plt.ylabel("Density")plt.tight_layout()
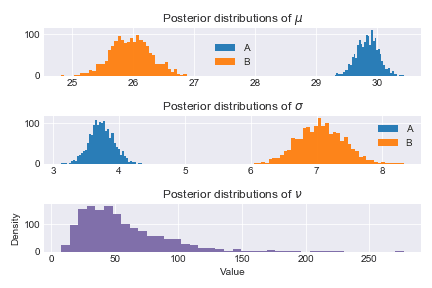
히스토그램에서 보듯이 A의 이용 시간이 B보다 훨씬 높음을 볼 수 있고, 우리가 세팅한 실제 평균 값인 mu_A=30, mu_B=26를 거의 비슷하게 추정함을 확인할 수 있습니다.
정확한 값을 보려면 utils.summary()를 사용합니다. 이 때 95% HPD (Highest Posterior Density) interval는 95%의 확률로 모수를 포함함을 의미합니다.
mcmc.summary()
이를 표로 정리하면 다음과 같습니다.
| 모수 | Mean | SD | MC Error | 95% HPD interval |
|---|---|---|---|---|
| 30.457 | 0.26 | 0.006 | [29.937,30.931] | |
| 25.505 | 0.447 | 0.01 | [24.612,26.363] | |
| 3.994 | 0.196 | 0.005 | [3.616,4.374] | |
| 6.828 | 0.347 | 0.011 | [6.144,7.483] | |
| 45.152 | 29.382 | 0.872 | [7.048,104.823] |
실제 값인 과 HPD interval을 비교해보면 모두 모수를 포함함을 확인할 수 있습니다.
MCMC 진단
MCMC sample이 잘 생성되었는 지 진단하는 방법은 pymc에 내장된 plot을 사용하면 됩니다.
MCMC sample들의 trace plot, auto-correlation, histogram을 확인할 수 있습니다.
이에 대한 자세한 내용은 StatLect Markov Chain Monte Carlo (MCMC) diagnostics에서 확인할 수 있습니다.
이 진단이 필요한 이유는 MCMC sample들이 정상성을 띠어야 사후 분포을 잘 근사했다 말할 수 있기 때문입니다.
MCMC sample들이 잘 생성되었다면
- trace plot이 구간 내에서 선이 위 아래로 왔다갔다 하는 모습을 보입니다.
- auto correlation plot은 sample의 lag에 따른 자기상관 관계를 그린 것으로, 오른쪽으로 갈수록 자기상관계수가 줄어드는 모양을 보입니다.
pm.Matplot.plot(mcmc)
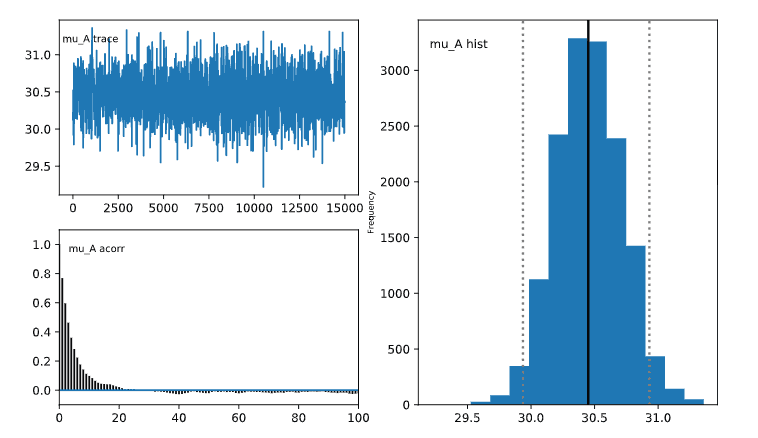
예를 들어 mu_A의 진단 플랏을 확인해보면
mu_A_trace에서 trace plot이 30과 32정도 사이에서 선이 위 아래로 왔다갔다 하는 모습을 보입니다.mu_A_acorr에서 auto correlation plot이 오른쪽으로 갈수록 자기상관계수가 줄어드는 모양을 보입니다.
그 외의 모수들도 모두 진단했을 때 큰 문제가 없었기 때문에 사후 분포의 추론 결과를 믿을 수 있습니다.
Reference
- Elia님의 AB 테스팅이란 무엇인가
- John K. Kruschke, Bayesian Estimation Supersedes the t Test
- 권정민님의 실무에서 활용하는 AB 테스트 발표자료
- 박장시님의 AB 테스트에서 p-value에 휘둘리지 않기
- pymc documentation
- pymc3 BEST Example
- StatLect Markov Chain Monte Carlo (MCMC) diagnostics
