본 글은 트리 앙상블(랜덤포레스트 등) 모형 대한 기본적인 이해를 전제로 하고, 베이지안의 MCMC 추론에 대해 알고계시면 이해에 큰 도움이 될 수 있습니다.

베이지안에게 랜덤포레스트는 살짝 아쉽다.

트리 앙상블 모형은 정형 데이터에서 예측을 위한 강력한 도구입니다. 개별 트리모형의 경우 분기 과정에서 불순도를 가장 줄일 수 있는 방향으로 준기 기준 변수와 그 값을 선정합니다. 만약 아직 데이터를 잘 설명하지 못했다면 더 분기하고, 지나치게 분기했다면 가지치기를 통해 복잡도를 낮춰주기도 합니다. 그리고 각 노드별로 속하는 데이터들의 값들의 평균을 그대로 예측값으로 사용하게 되죠. 랜덤포레스트나 부스팅 계열의 트리 앙상블 모형은 이런 개별 트리들을 합쳐서 더 복잡한 관계를 효과적으로 근사하기 위한 방법입니다. 랜덤포레스트는 복수의 이질적인 나무모형을 적합해서 평균을 내는 방식이라면, 부스팅을 약한 학습기 (weak learner)를 더해가는 방식이라는 사실을 알고 있습니다.

랜덤포레스트나 부스팅 같은 기존의 트리 앙상블 모형은 예측, 즉 점추정에 대해서는 아주 훌륭한 모형입니다. 하지만 예측의 불확실성(분산)에 대한 정보들을 충분히 갖고있진 못합니다.

만약 예측의 불확실성까지 트리모형을 통해 얻고 싶다면 어떻게 해야할까요? 예측의 불확실성, 즉 분산에 대한 정보를 알고 싶다면 우리가 다룰 수 있는 확률 모형 프레임워크를 동원해야 하고, 이를 위한 가장 자연스러운 방법이 “베이지안” 입니다. 베이지안 스타일로 나무모형을 적합하면 예측의 불확실성이라는 핵심적인 목표 뿐만 아니라, 변수 중요도 같은 부가적인 사항도 같이 달성할 수 있습니다. 그래서 이번 글에서는 베이지안 트리 모형, 그리고 그것으로 만들어지는 BART (Bayesian additive regression trees, 베이지안 가법 회귀 나무)에 대해 소개하고자 합니다. 먼저 BART를 요약할 수 있는 3가지 특성들에 대해 설명하고, 필요하신 분들을 위해 살짝의 수식을 덧붙이겠습니다.

1. BART는 모든 선택이 확률적이다.

기존의 모든 과정이 결정적 (deterministic)이었던 트리모형과 달리 베이지안 트리 모형은 모든 결정이 확률적 (stochastic) 입니다. 이전에 나무 모형들에서는 고려해주지 않았던 부분들을 모두 확률적인 표현으로 대체해줍니다. 나무가 깊어지면서 더 분기할지에 대해 확률적으로 선택하고, 이때 나무가 깊어질수록 해당 노드에서 분기할 확률을 낮춰주는 방식으로 작동합니다. 어떤 변수를 기준으로 분기할지에 대해서는 주어진 변수들 중 무작위로 1개를 선택하고, 해당 변수안에서도 무작위로 하나의 데이터를 선정하여 해당 값을 기준으로 분기합니다.

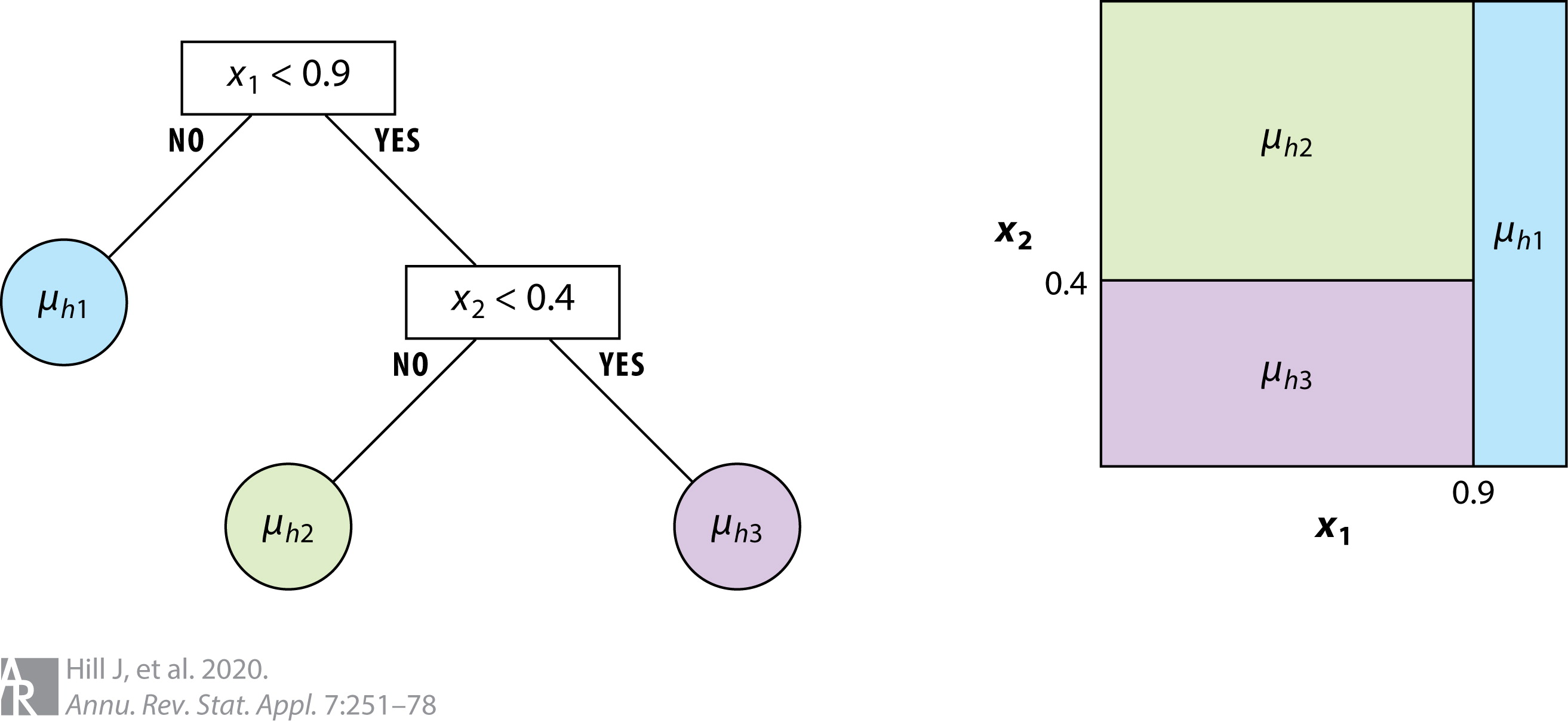
이렇게 만들어진 하나의 트리 구조 안에서 예측을 진행하는 과정도 확률적입니다. 특정 노드 안에서 속한 데이터들이 있다고 했을 때, 기존의 트리 모형은 y값들의 평균을 예측값으로써 사용했습니다. 하지만 베이지안 트리모형은 y값들의 평균을 중심으로 두는 정규분포에서 샘플링을 진행하고, 샘플링을 통해 얻어진 값을 예측값으로 사용합니다. 그냥 y값들의 평균을 쓰지 왜 그렇게 복잡하게 하는지 부자연스럽다고 생각할 수 있지만, 해당 과정을 통해야만 예측의 불확실성을 “자연스러운” 형태로 표현할 수 있습니다.

더불어 한 번 확률적으로 정해졌다고 끝나지 않습니다. 베이지안 모형은 MCMC라는 과정을 통해 사후분포를 따르는 샘플들을 얻게 되는데, 이 과정에서 트리구조와 예측 모수들은 계속 바뀔 수 있습니다. MCMC 과정마다 나무를 1) 추가적으로 분기할지, 2) 가지치기를 시행할지, 3) 분기 기준 변수를 변경할 지 확률적으로 선택합니다. 이렇게 바뀐 나무구조를 바탕으로 다시 예측값을 정규분포에서 샘플링합니다.

2. BART는 베이지안 트리 앙상블 모형이다.

BART는 확률적으로 생성되는 트리모형들을 여러개 더한 형태의 모형으로, 랜덤포레스트와 부스팅 같은 트리 앙상블 모형에 대해 베이지안 버전입니다. 그래서 기존의 트리모형이 갖는 특징들을 그대로 가져오게 되고, 이를 바탕으로 이해하는 것에 무리가 없습니다.

BART는 확률적으로 생성되는 트리 모형들을 여러개 더한 형태의 모형으로, 기존의 트리들을 더해서 만들어진 모형들과 매우 유사합니다. 기존의 랜덤포레스트와 부스팅 계열 모형들처럼, Bias-Variance tradeoff의 적정선을 찾기 위한 시도입니다. 베이지안 트리 모형들을 여러개 적절하게 더함으로써 과적합을 피하면서도 좋은 예측력을 보여줍니다.

BART는 그중에서도 부스팅 계열 모형에 가까워서, 저는 BART를 다른 사람들에게 소개할 때 “베이지안 부스팅” 모형이라고 퉁쳐서 표현하기도 합니다. 물론 부스팅 모형의 베이지안 스타일이라고 대응시키기에 어려운 면이 있지만, 적어도 약한 학습기 (weak learner)들의 합으로 표현되는 점은 유사한 것 같습니다. BART도 각각의 나무들이 갖는 영향력이 너무 커지지 않도록 모형이 설계되어 있고, 모형 적합 과정도 이를 충분히 반영하고 있습니다.

1) BART의 각 나무는 너무 깊이 분기하지 않습니다. 나무의 각 깊이에서 분기 여부를 결정할 때, 나무가 깊으면 추가적으로 분기할 확률이 다음과 같이 빠르게 감소합니다. $d_{\eta}$는 $\eta$ 노드의 깊이를 표현합니다.

2) 더불어 나무가 갖는 영향력을 완전히 등확률로 $1/H$처럼 정의하긴 어렵더라도, 나무의 개수 $H$가 커질수록 각 나무의 영향력이 더 약해지도록 통제하는 것이 가능합니다.

3) 살짝 어려운 설명을 추가하자면, 이런 weak learner의 특성이 반영될 수 있도록 역적합 (backfitting) 방식으로 모형을 적합합니다. $j$번째 나무를 제외한 나머지 나무들로 만들어진 잔차 $R_j$를 다음과 같이 정의하겠습니다.

이렇게 얻어진 잔차 $R_j$를 활용해서, BART에서 각각의 $j$번째 나무 $g(x; \mathcal{T}_j, \mathcal{M}_j)$들은 MCMC 과정시에 $R_j$만 잘 맞출 수 있도록 트리구조와 예측모수를 변경해나갑니다.

3. BART는 예측의 불확실성을 계량할 수 있다.

확률적인 트리를 앙상블함으로써 얻을 수 있는 가장 중요한 효과는 예측의 불확실성을 계량할 수 있다는 점입니다. 계산적인 이슈가 존재함에도 베이지안 모형이 필요한 이유는 예측의 불확실성이 중요한 문제들이 많다는 것이겠죠. 기존의 랜덤포레스트나 부스팅도 일부 이런 정보를 제공하긴 하나, 해당 모형은 분류문제에서 예측 확률이 다소 0과 1에 치우치게 분리하려는 특징이 있어, 불확실성의 정보도 정확하지 않을 수 있다는 문제를 갖고 있습니다. 그래서 BART를 통해 얻을 수 있는 정보가 더 소중합니다.

MCMC 과정에서 얻은 100개의 BART 샘플을 다음과 같이 $f^{*}_1, \ldots, f^{*}_{100}$이라고 합시다. 그러면 BART의 경우 특정 $x$가 들어왔을 때의 예측값으로 다음과 같이 $f^{*}$들의 평균을 사용할 것입니다.

해당 예측에 대한 불확실성은 95% 신용구간을 구함으로써 얻을 수 있는데, $f^{*}_1(x), \ldots, f^{*}_{100}(x)$의 크기를 줄 세우고 상위 및 하위 2.5% 값을 구하는 것입니다.

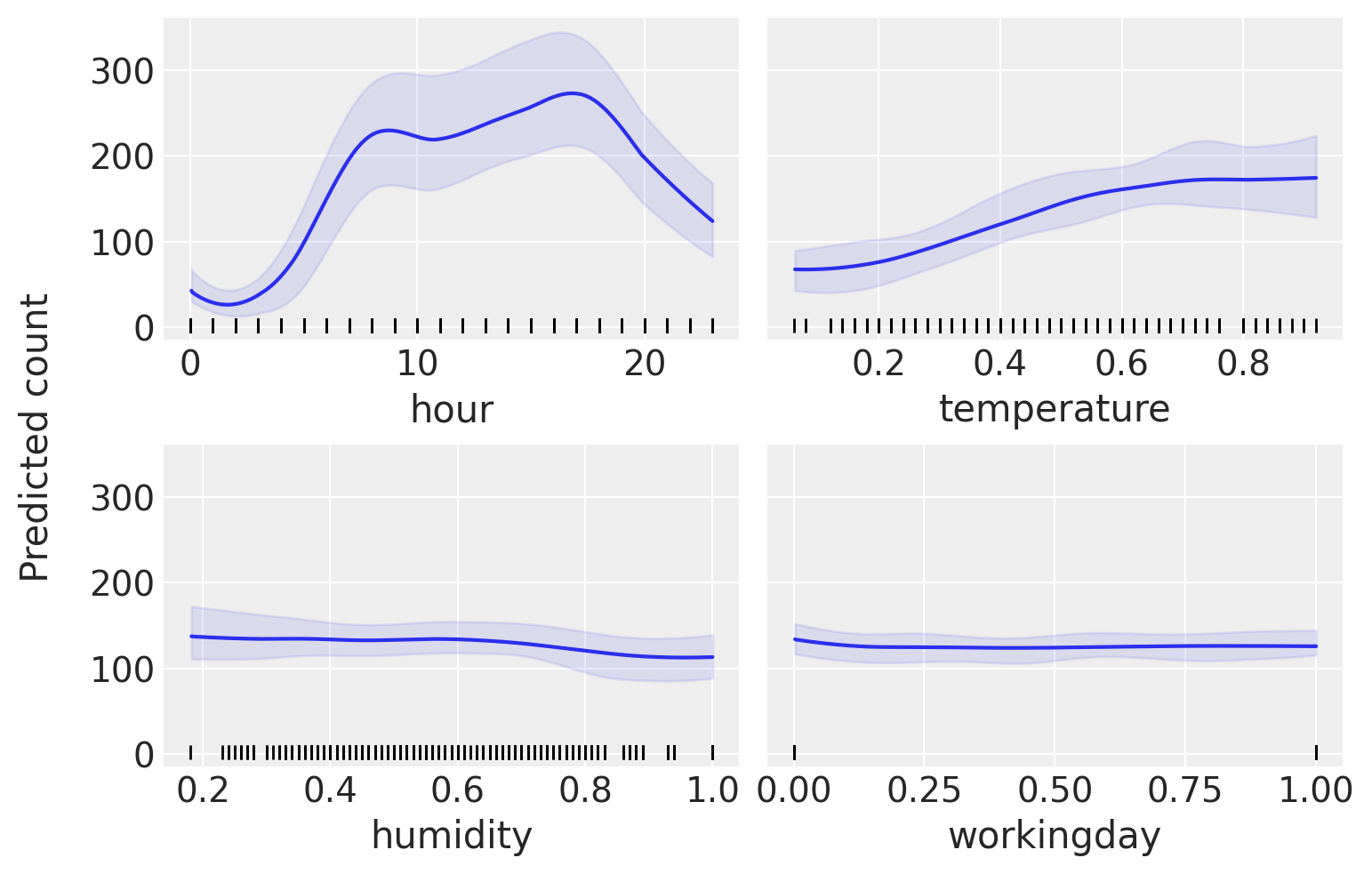
얻어진 샘플들 통해 변수중요도나 변수에 따른 예측값의 변화를 구하는 것도 추가적인 과정이 필요하지 않습니다. 변수중요도의 경우 샘플링을 진행할 때 해당 변수가 나무의 분기기준으로 얼마나 쓰였는지를 카운트하는 것으로 표현될 수 있습니다. 분기 기준 변수 자체를 무작위로 선정되지만, 해당 기준이 “그럴듯”해야 최종적으로 허용되기 때문에 이는 합리적인 방법입니다. 더불어 MCMC 과정에서 얻어진 샘플들을 , 관심 변수의 변화에 따른 예측값의 변화를 PDP (partial dependence plot)를 통해 시각화해서 확인하는 것이 가능합니다.

BART의 수식적 표현

이 부분은 BART에 대한 수식적인 표현을 담고 있습니다. 넘어가셔도 괜찮습니다.

해당 내용은 BART를 처음 소개한 논문인 Chipman (2010)을 기반으로 합니다.

1) 가법 나무 (additive trees) 모형

BART는 수식적으로는 다음과 같은 가법 나무의 형태를 지닙니다.

여기서 $f(\cdot)$은 우리가 찾고 싶은 함수입니다. 다음의 $f(\cdot)$를 근사하는 함수를 $g$라는 베이지안 트리모형을 $H$개 더해서 만들고자 합니다. 각각의 트리모형은 트리구조 $\mathcal{T}_h$와 트리 구조안에서의 각 터미널 노드의 예측 모수들 $\mathcal{M}_h = \{ \mu_1, \ldots, \mu_{n_{h}} \}$로 표현됩니다. 트리구조 $\mathcal{T}_h$는 나무의 깊이, 분기에 사용된 변수, 분기에 사용된 값을 포함합니다.

2) 규제 사전분포

BART는 여기서 정의한 모수들에 대해 모두 사전분포를 부여함으로써, 트리모형을 확률적인 표현의 대상으로 가져옵니다. 생략을 거쳐, 다음의 모수들 $\mathcal{T}_h, \: \mu_{n_h}|\mathcal{T}_h, \: \sigma^2$ 대해서만 사전분포를 부여하면 충분합니다. 트리 구조 $\mathcal{T}_h$의 나무 깊이는 이전에 위에서 말씀드린 대로 $\alpha (1+d_{\eta})^{-\beta}$를, 분기 기준 변수와 값은 균등 (uniform)하게 샘플링합니다. 일반성을 잃지 않는 선에서 y값을 $[-0.5, 0.5]$로 조정해주면, 예측 모수 $\mu_{n_h}|\mathcal{T}_h$에 대한 사전분포를 $N(0,\sigma_{\mu}^2)$로 평균이 0인 정규분포에서 샘플링하는 것이 가능합니다. $\sigma_{\mu} = 0.25 * \sqrt{H}$로 설정합니다. 오차의 분산 $\sigma^2$은 켤레성 (conjugacy)를 만족시켜줄 수 있도록 역감마분포로 설정합니다.

3) 사후분포 추론

각 나무들에 대해 1) 역적합 방식으로 2) 블록화 깁스 샘플링을 진행합니다.

트리구조가 MCMC 과정에서 계속 바뀌면서 사용되는 예측 $\mu$의 개수가 변하는데, 이는 MCMC의 수렴에 큰 영향을 미칩니다. 따라서 예측모수의 차원과 무관하게 MCMC를 진행할 수 있도록 블록화해줍니다. 그에 따라 다음의 샘플링을 나무별로 반복하면 됩니다.

각각의 세부적인 업데이트 형태는 Chipman (2010) 혹은 Kapelner (2016)에서 참고할 있습니다. 오차의 분산 $\sigma^2$은 켤레성을 만족하므로, 역감마분포에서 바로 샘플링하는 것이 가능합니다.

Hi BART! 내 예측의 불확실성을 알려줘

BART의 경우 부스팅 모형 대비 하이퍼파라미터 튜닝에 민감하지 않습니다. 부스팅은 학습률부터 다양한 하이퍼파라미터들을 조정해주는 과정이 중요할 수 있는데, BART의 하이퍼파라미터는 사전분포의 형태를 결정하는 것이기 때문에 상대적으로 조정에 둔감합니다. 따라서 BART 자체 적합은 다른 부스팅 모형보다 오래 걸릴지라도, 튜닝에 소요되는 시간까지 고려한다면 큰 차이가 존재하지 않을 수 있습니다. 더불어 기본적으로 MCMC는 병렬처리에 친화적인 계산방법은 아니지만, 최근에는 병렬처리까지 포함하는 BART 알고리즘이 존재하며 R은 이를 기반으로 짜여져 있습니다. 아쉽게도 PyMC에는 2023년 4월 기준 적용되있지 않은 것 같네요.

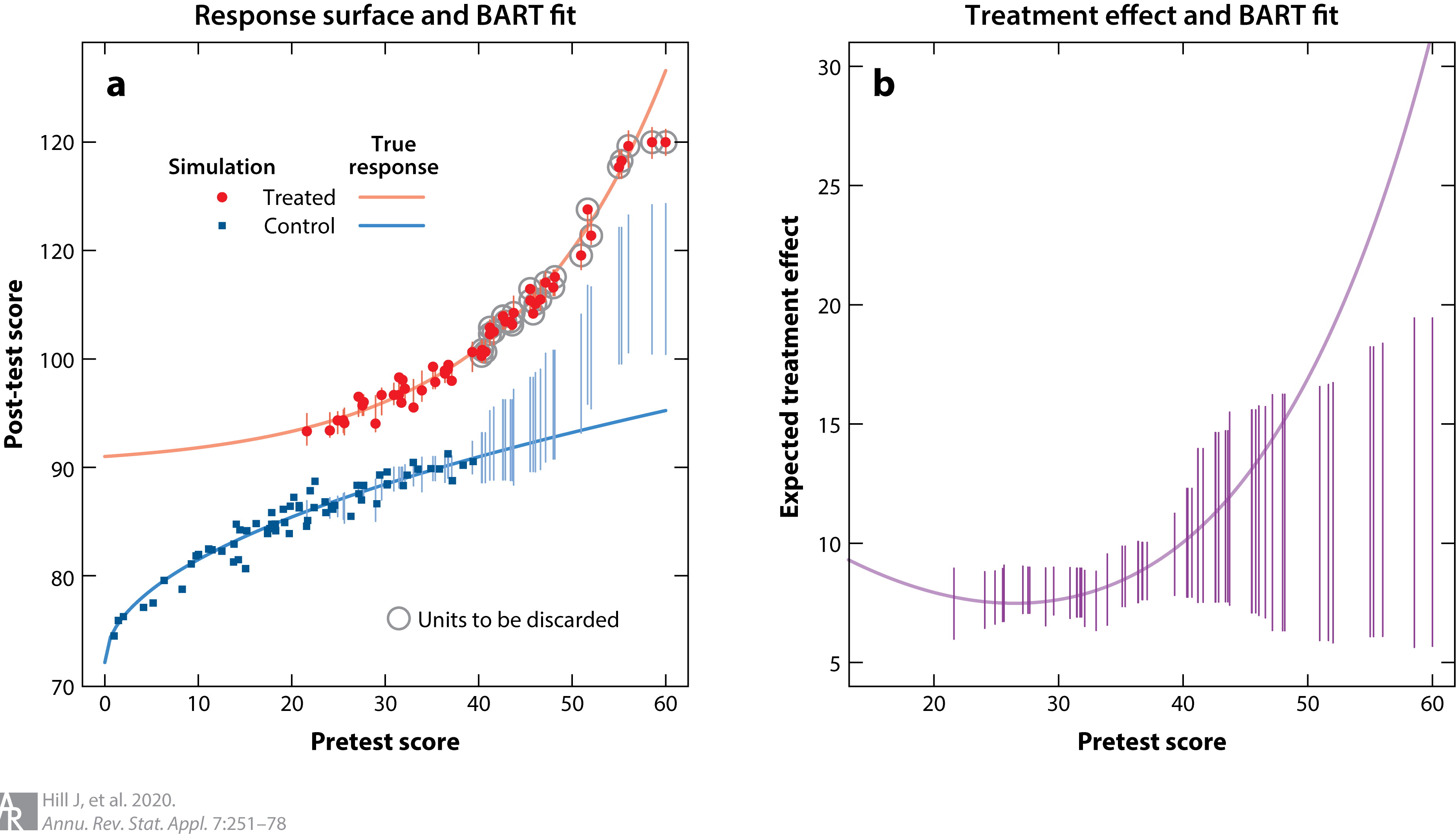
BART의 경우 복잡한 함수를 잘 근사할 수 있으면서도 불확실성에 대한 계량이 가능하기 때문에 여러 도메인으로 확장될 여지가 많습니다. 특히 최근에는 관찰데이터에 대한 인과추론에 BART를 사용하는 경우들이 많습니다. 인과추론의 경우 가정을 기반으로 하기 때문에, 추론의 결과가 얼마나 강건한지, 우연에 의한 것 (casual causal inference)은 아닌지를 확인할 필요가 있습니다. 이때 BART를 통한 예측과 추론이 효과적일 수 있습니다. 위의 그래프는 BART를 처음 인과추론에 적용한 논문의 일부를 더 보기 좋게 수정한 그래프인데, 수직선이 BART 추론의 불확실성을 표현하는 부분입니다. 통제군 (control)의 데이터가 없는 부분에서 불확실성이 커지는 것을 확인할 수 있죠?

BART를 한 마디로 요약하자면, 불확실성을 말해줄 수 있는 트리 앙상블 모형입니다. BART가 늘 필요한 것은 아니지만, 단순 예측 결과 뿐만 아니라 불확실성에 대한 정보가 필요할 경우가 있다면 사용해보는 것은 어떨까요?

참고자료

• Python BART 적용 코드 예제
• R BART 적용 코드 예제
• Hill, Jennifer & Linero, Antonio & Murray, Jared. (2020). Bayesian Additive Regression Trees: A Review and Look Forward. Annual Review of Statistics and Its Application, 7.
• Hugh A. Chipman, Edward I. George, Robert E. McCulloch. (2010). BART: Bayesian additive regression trees. The Annals of Applied Statistics, 4(1), 266-298.
• Kapelner, A., & Bleich, J. (2016). bartMachine: Machine Learning with Bayesian Additive Regression Trees. Journal of Statistical Software, 70(4), 1–40.