들어가기에 앞서

일을 하면서 그리고 생활 속에서도 우리는 다양한 숫자들을 마주하게 되는데요. 혹시 그 숫자들에 속고 있다는 생각을 해보신 적은 없으신가요?
이번 글에서는 우리가 일상에서 마주하게 되는 그리고 회사에서 업무를 하면서, 데이터 분석 결과를 확인하면서 흔히 속게 되는 데이터의 함정들에 대해서 알아보려고 합니다.

평균이라는 함정

종종 신문을 보다 보면 평균 연봉에 대한 기사를 볼 수 있는 데요. 그 기사를 보면서 내 연봉을 비교해보고 자괴감에 빠지다가, “뭐 평균이라 그렇지 누군가 한 명이 엄청 큰 연봉을 받고 있는 걸 거야”. 라고 생각하며 정신을 차릴때가 있는데요.

평균이라는 게 분명 가장 많이 그리고 흔히 쓰이는 대표값이라는 사실에는 누구도 반론의 여지는 없겠지만, 또 평균이 현상을 정확하게 설명해주지 않는 다는 사실 역시 많이 알고 있을 거에요.

우선 아래의 예시를 한 번 살펴면서 자세히 얘기해 볼 게요.

✔︎ A사 : 평균 연령 32세, 평균연봉 8,000만원
✔︎ B사 : 평균 연령 35세, 평균연봉 5,100만원

이 두 기업의 정보를 훑어 봤을 때 어떤 기업에 더 가고 싶으신가요? 혹은 어떤 기업이 더 좋아보시나요?
아마 A사가 더 젋고, 연봉도 높아보이니 훨씬 좋은 회사라고 생각하게 될 거 같은데요. 이렇게 생각하는 게 정말 올바른 해석일까요?

데이터를 쪼개보면 어떨까요?

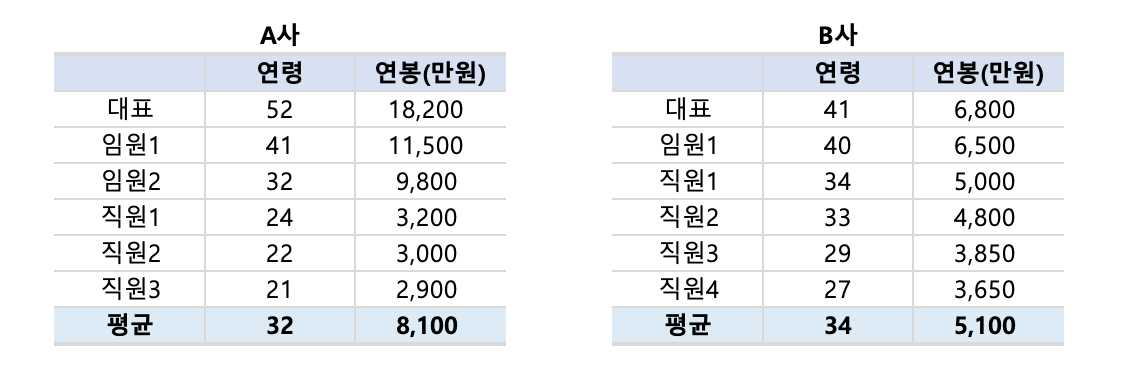
평균은 A사가 훨씬 높지만, 실상은 임원들을 빼면 대다수 20대 초반의 젊은 직원들의 연봉은 대표의 1/5에도 못미치죠.
평균으로 봤을 때는 훨씬 좋아보이던 A사가 실상은 그렇지 않다는 걸 알 수 있는데요. 오히려 B사가 괜찮게 느껴지실거에요. 이렇듯 단순히 평균만으로 판단했을 때에는 해석의 오류가 생길 여지가 있습니다.

평균이 분명 가장 널리 사용되는 대표값이긴 하지만, 그 외에 ‘중앙값’이나 ‘최빈값’이라는 말도 들어보셨을 거에요.
중앙값은 수치 집합의 원소를 작은 순부터 큰 순서대로 정렬했을 때 가운데에 위치하는 값인데요. 위의 이미지로 생각하면 A사의 경우 임원2와 직원1의 연봉의 평균인 6,500만원이 되겠네요. B사의 경우는 4,900만원이 되구요. B사의 경우는 큰 차이가 없지만 A사의 경우는 그래도 평균과의 차이가 꽤 나게 되죠.
최빈값은 수치 집합의 원소가 가장 많은 원소가 포함된 범위의 값이라고 생각하면 됩니다.
이런 다른 대표값들도 같이 확인해야 평균이 주는 함정에서 빠져나올 수가 있죠.

대표값인 평균은 진실을 ‘잘’ 요약해 주지만, 모든 진실을 완벽하게 반영하는 것은 아니라는 점을 기억해야 합니다

심슨의 역설로 알아보는 또 다른 함정

통계의 함정과 약간은 비슷할 수 있는 또 다른 함정이 있는데요. 바로 심슨의 역설(Simpson’s Paradox)입니다.

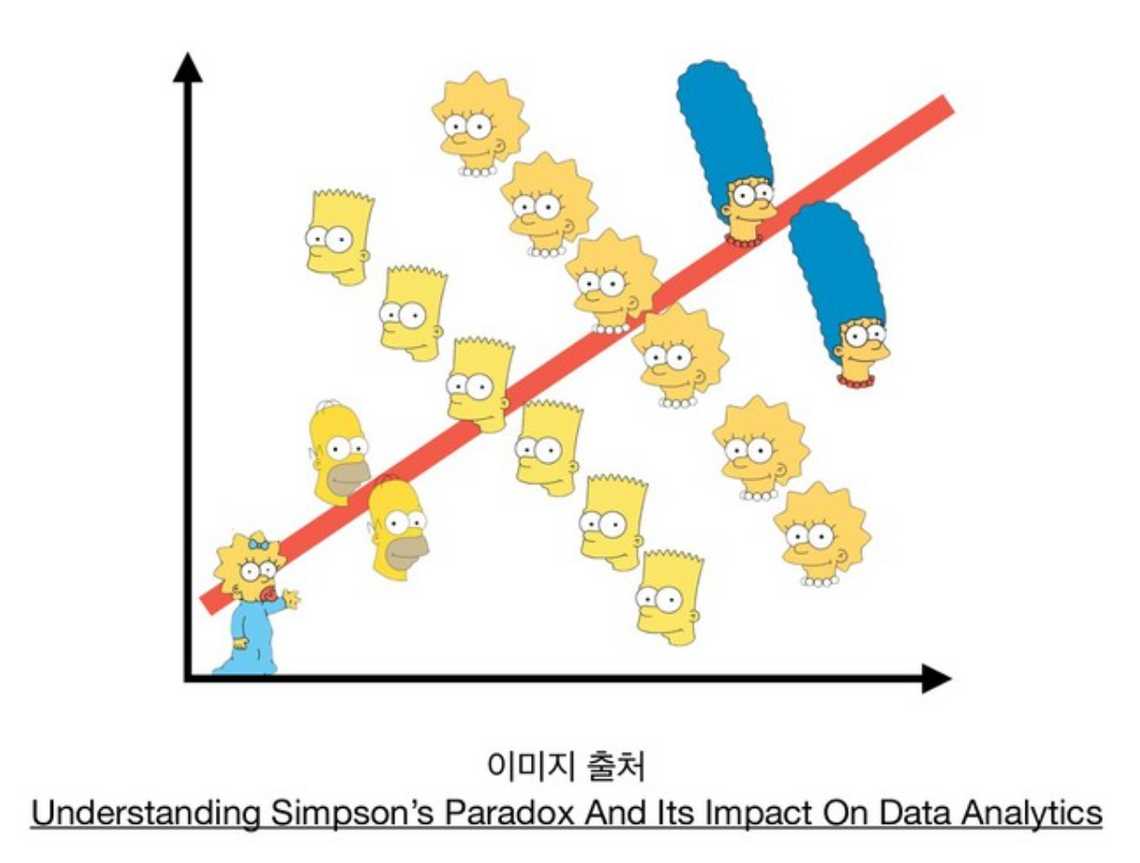
심슨의 역설은 여러 부분 그룹의 자료를 합했을 때의 결과와 각각 부분 그룹의 결과가 다른 때를 말하는데요. 그 결과가 부분의 결과와 달라지는 결과가 발생하는 것은 일반적인 상식으로는 쉽게 이해가 되지 않으므로 Paradox라고 합니다.

신장결석 치료에서의 예시를 보면서 얘기해 볼게요

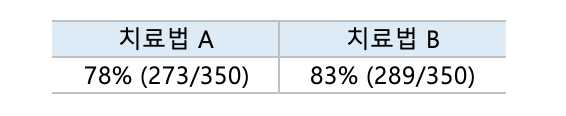
위 테이블을 보고 어떤 약물이 더 효과적인가라고 묻는다면, 다들 '치료법 B가 더 효과적이다'라고 답할텐데요. 하지만 이 테이블에 부분 그룹에 대한 변수(신장 결석의 크기)를 추가하여 좀 더 자세히 살펴보면 얘기가 달라질 수 있습니다.

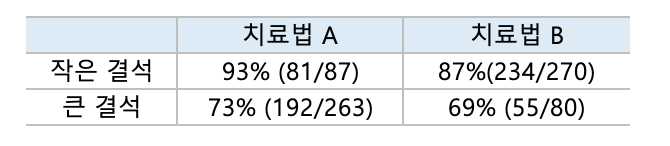
신장 결석 크기에 따른 각각의 치료법의 효과인데요. 위의 결과를 보고도 치료법 B가 더 효과적이라는 말을 할 수 있을까요?
이렇게 세부 변수까지 확인했을 때에는 결석의 크기가 작거나 큰 상황 둘 다에서 치료법 A가 치료법 B보다 효과적이라는 결론을 얻을 수 있죠.
그리고 이러한 변화의 차이는 시도가 많았던 그룹이 전체의 평균을 좌우하게 되면서 벌어지는 현상이라고 볼 수 있습니다.
결과적으로 세부 변수를 확인하지 않고 데이터를 통합해서 확인하게 되면 원래 결과와는 전혀 다른 의미를 도출하는 오류를 범하게 되는 것을 확인할 수 있죠.

내 프로덕트의 지표를 분석한다고 생각해보면, 자주 고민하게 되는 문제중 하나일 텐데요. 매일매일 지표가 나가는 데 이걸 일주일 합산을 보고 싶다고 한다면, 이미 계산된 데일리 지표의 평균을 일주일치 모아서 다시 평균해서 나갈지 아니면 일주일치의 데이터를 모두 합해서 평균을 새로 계산해야 할 지에 대한 고민이과 비슷하다고 생각되는데요.
매일매일의 지표를 평균하면 그 매일의 성과가 평균이 되어서 나가는 것이 되고, 일주일치를 다 합산해서 평균을 다시 구하게 되면 일주일 중에 클릭이 많거나, 전환이 많았던 날, 혹은 배속이 유난히 많았던 날이 전체 평균을 좌우하게 되겠죠.

데이터의 세부 변수들을 확인하지 않는 다면 의도했던 결과와는 전혀 다른 결론을 내릴수 있다는 점을 명심해야 합니다

선형적인 사고의 오류

우선 내가 회사의 차량 개발 담당자라고 생각해볼게요. 회사의 주요 제품은 1리터에 10km을 달리는 SUV차량과 1리터에 20km을 달리는 세단 차량이 있다고 가정 해보겠습니다. 요즘 대세인 ESG를 따라가기 위해 기존 제품의 연비를 절감하는 목표를 할당 받았다고 생각해볼게요.

아래의 상황을 봤을 때 어떤 모델을 업그레이드 하는 게 좋을까요?

A. 연비가 10km/ℓ인 SUV를 20km/ℓ로 향상시킨다
B. 연비가 20km/ℓ인 세단은 50km/ℓ로 향상시킨다

위의 문장만 놓고 직관적으로 생각해본다면 B가 더 좋은 결정이라는 생각이 들거 같은데요. 연비의 상승폭으로 볼 때 30km/ℓ의 증가가 10km/ℓ증가 보다 훨씬 크기 때문이죠. 백분율로 생각해도 100% 향상인 A의 결과보다, 150% 향상되는 B의 결과가 더 좋아보입니다.

정말 이게 최선의 판단일까요?

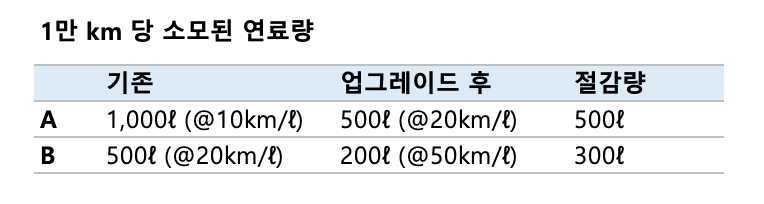
실제로 계산을 해보면 1만 km를 달렸을 때 A는 500ℓ를 아끼게 되지만, B는 300ℓ를 아끼는 데 그치는 것을 알게 되는데요. 결과를 보고 다소 의아해 할 수도 있을 것 같은데 이는 우리의 두뇌는 일반적으로 선형적(linear)인 사고를 하기 때문입니다.

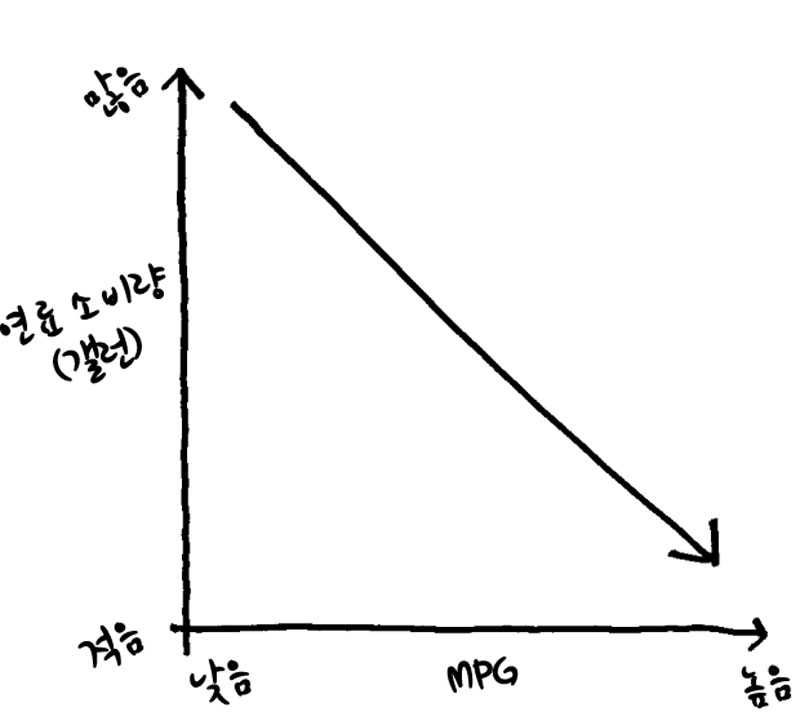
처음 상황을 봤을 때 우리는 위의 그림처럼 생각을 하게 되는 것이죠. 하지만 이 그래프는 정확하지 않습니다. 연료 소비량과 연비는 선형적인 함수관계가 아니기 때문이죠. 실제로 계산해 보면 그래프는 아래와 같은 모습을 확인할 수 있습니다.

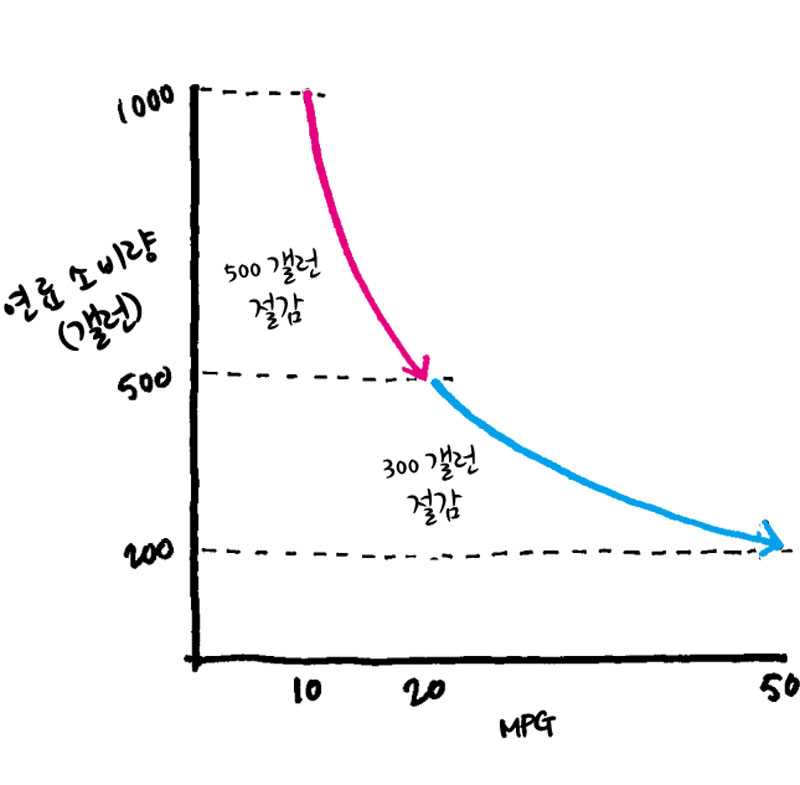
기술 개발 초기의 개선은 약간의 개선으로 큰 효과를 볼 수 있지만, 어느 정도 기술이 완숙해진 이후에는 초기와 비슷한 개선 효과를 얻기 위해서는 초기와는 비교할 수 없을 정도의 많은 양의 노력과 시간이 투입되어야 한다는 사실을 경험적으로 알고 있을 거라고 생각하는데요. 이렇듯 대부분의 현실에서의 문제는 선형적이기 보다는 비선형적인 경우가 많습니다.
하지만 실제 숫자를 보게 되었을 때 우리는 단순히 숫자의 관계를 보고 선형적으로 사고하고 결정하려고 하죠.

결국 단수히 숫자의 관계를 보고 대략적으로 파악하는 게 아닌 실제로 계산해보고 또 시각화해 그려보면서 데이터들의 관계를 파악해야 할 필요가 있습니다.

마치며…

데이터나 수치들을 통한 생각들을 할 때 흔히 빠질수 있는 몇가지 함정들에대해서 살펴보았는데요. 이번 글을 작성하면서 생각보다 쉽고 흔하게 수치들이 주는 함정에 빠져서 잘못된 결론을 내리는 경우들이 있다는 생각이 들었습니다. 어떤 데이터를 접하게 될 때 단편적으로 바라보고 결론을 내는 게 아니라 좀 더 다양한 관점에서 데이터를 뜯고 맛보아야 할 것 같다는 생각이 드네요.
위의 내용들을 좀 더 자세하게 확인하고 싶다면 글을 쓰면서 주로 참고한 아티클 목록을 아래 작성해두었으니 살펴보아도 좋을것 같습니다.

[참고자료]

• Linear Thinking in a Nonlinear World, Harvard Business Review, by Bart de Langhe, Stefano Puntoni, and Richard Larrick
• 심슨의 역설, 데이터야놀자 2019, 윤선미