Table Of Contents
1. 개요
작년 하반기 나는 Retention 지표 향상을 목표로 하는 목적조직에 소속되어있었다. Retention을 올리는 궁극적인 목적은 유저의 LTV(Lifetime)를 향상하여 서비스의 체질 개선을 하는 것이 목적.
당시 Data Analyst 였던 나에겐 Retention 상승에 따라 LTV가 어떻게 상승하는지 시뮬레이션 해달라는 과제가 주어졌다. (TMI: 저는 현재 Product Manager 직무를 수행하고 있습니다.)
이번 글에서는 이 과제를 수행하면서 썼던 분석을 소개하고 회고하고자 한다. 특히 스타트업 환경인지라 빠른 의사결정을 위해 분석했기에 스타트업 분석가 분들과 실무를 공유하고 싶은 마음이다. 또 실무에서 적용 가능하도록 글을 써보려 한다.
2. LTV (Lifetime Value, 고객 생애 가치) 지표 설명
LTV는 수익화 분석의 궁극적인 지표로 유저 한명 당 평균적으로 install 후 이탈할 때까지 전체 활동기간(Lifetime)에서 누적해서 발생시킨 기대 수익(Lifetime Revenue)으로 정의할 수 있다. 쉽게 말해 1인 당 서비스 이용하면서 총 얼마 쓰는지에 대한 지표다. 이를 확인하고 Acquisition Cost와 비교를 통해 비즈니스의 수익화를 분석할 수 있다.
LTV를 계산할 수 있는 공식은 여러가지가 있지만 이번 글에서는 아래와 같은 공식을 사용하였다.
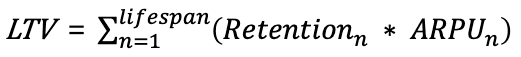
- 설명: n-day retention과 그 n-day에서의 ARPU(Average Revenue per User) 곱을 0<=n<=lifespan에 따라 n+1 반복할 때 모두 더한 값이다. 여기서 n-day, 즉 daily 기준으로 써놨는데, 이는 산업 및 서비스에 고유 특성에 따라 다르다. lifespan도 마찬가지로 서비스 특성에 따라 다르다. 어떤 서비스는 365일이 총 lifespan이 될수 있고, 어떤 서비스는 700일이 총 lifespan이 될 수 있다. 이는 도메인 지식이 필요하다. (이 글에서는 임시적으로 daily 기준으로, lifespan은 700일로 소개한다. 700일인 이유는 보안상 실제 사용한 데이터를 사용할 순 없어 아무 숫자나 찍었다.)
- 이를 좀 더 단순화 하면 Lifetime * 평균 ARPU 으로 표현 가능하다.
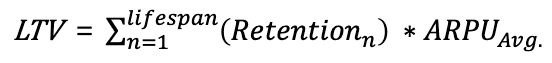
LTV 공식 1
3. 분석 방법론
Retention 변화에 따른 LTV 시뮬레이션을 위해 디자인한 분석 방법론은 아래와 같다.
- LTV를 Lifetime과 평균 ARPU의 곱의 함수로 분해한다.
- Retention 데이터를 추출하고, lifespan이 700일이므로 Day-700 Retention을 예측된 로직을 통해 계산한다.
- 2번에서 구한 Day-700 Retention으로 Lifetime을 구한다. 이때 구하는 과정은 엑셀을 활용하며 전부 수식으로 계산 되도록 만들어 추후 Retention-LTV 변화를 시뮬레이션 할 때 사용한다.
- 평균 ARPU를 구한다.
- 평균 ARPU를 고정값으로 두고 Retention 1%p 오를 때 Lifetime의 결과 값과 평균 ARPU를 곱하여 LTV 변화를 시뮬레이션한다.
이렇게 방법론만 보고는 이해하기 어려울 것 같다. 아래 분석 상세를 소개하고자 한다.
4. 분석 상세
4-1 Lifetime 계산
유저의 1인당 기대 Lifetime은 Day0~700 Retention의 합이다.
n-day retention은 n일차에 유저가 잔존할 확률이며, 바꿔 말하면 대상 코호트 유저의 n일차의 평균 일수다. day7 retention이 0.2 라면 대상 코호트 유저의 7일차 기대 일수는 평균적으로 0.2일이라고 보면 된다. 따라서 Day0부터 Day700까지의 701개의 리텐션 값을 모두 더 하면 1인당 평균 기대일수, 즉 구하고자 하는 1인당 전체 활동기간(Lifetime)을 구할 수 있다.
필자의 경우 Retention은 Amplitude에서 제공하는 차트를 통해 쉽게 추출할 수 있었다. 하지만 Day700 Retention까지 실측된 데이터를 구할 순 없다. 실측된 데이터를 사용하려면 거의 2년 전에 가까운 데이터를 사용해야하기 때문이다. 리텐션의 최신성을 반영해야 하기 때문에 Day0~Day30 실측 Retention 데이터 정도를 추출하고 나머지 Day31 Retention ~ Day700 Retention은 예측을 하기로 했다.
이때 나머지 n-day retention의 예측은 선형회귀를 통해 추정 가능하다. Retention 지표는 초반에 변화가 크고 이후에는 매우 조금씩 감소하는 것이 일반적이고, 경험적으로 “거듭제곱 함수” 형태를 통해 증가하며 실제로 실무에서 많이 활용되는 함수이다.
엑셀로 쉽게 설명하자면 차트의 추세선을 그릴 때 제공하는 옵션인 “거듭제곱 함수”를 통해 예측할 수 있다. Day0~Day30 실측 Retention을 visualization 한 후 [차트 요소 추가] > [추세선] > [추세선 서식]에서 제공되는 옵션 중 [거듭 제곱]이 있다. 아래 캡처 화면 처럼 거듭제곱 함수를 사용하면 꽤 훌륭한 fitting이 가능하다. R-square와 수식은 차트 옵션을 통해 차트 �위에 표현 가능하다. 인과를 분석하는 것이 아니므로 높은 R-square를 보고 fitting을 판단할 수 있다. 여기서 실측+예측된 데이터 포인트들을 모두 더하면 구하고자 하는 Lifetime을 구할 수 있다.
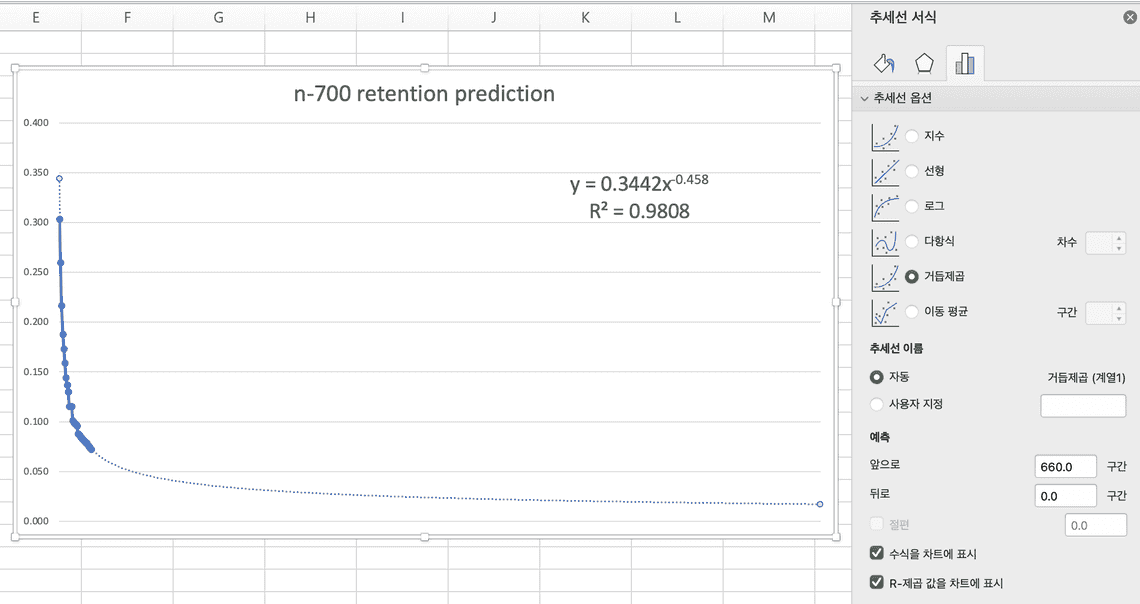
애석하게도 엑셀은 차트에 표현되는 수식의 정확한 값을 셀로 불러올 수 있는 기능은 제공하지 않는다. 따라서 함수를 통해 이를 직접 계산해야한다. 이는 선형회귀를 통해 추정 가능하므로 LINEST(known_y’s, known_x’s) 함수를 통해 계산할 수 있다. LINEST 함수는 least suare 방법을 통해 선형함수의 coefficient 값과 상수항을 자동으로 뱉어준다.
함수를 구하기 위해 known_y’s에는 Day0~Day30 실측 Retention이 known_x’s에는 1~30의 배열을 활용하면된다. 구하고자 하는 함수는 거듭제곱 함수의 형태이므로 y, x에 자연로그 ln을 씌워준다. 즉 LINEST(ln(known_y’s), ln(known_x’s)).
이 함수는 선형 함수의 coefficiet와 상수항 값을 나란히 뱉어내고 이를 통해 차트에 보이는 수식과 같이 x의 기울기와 지수 값을 구할 수 있다. 기울기는 상수항에 exp를 해준 값, 지수는 coefficiet 값이다.
수식을 구하게 되었으면 700일까지의 Retention을 예측하고 30일까지의 리텐션 실측값 31~700일까지 리텐션 예측값을 모두 더하여 Lifetime을 계산한다.
4-2 평균 ARPU 계산
LTV를 Lifetime과 평균 ARPU의 곱의 함수로 분해하였고, Lifetime을 구했으니 여기에 평균 ARPU를 곱하면 LTV를 구할 수 있다. 평균 ARPU는 분석 기간의 매출 총합을 AU 수 총합으로 나눈 값이다.
4-1에서 구한것과 비슷한 방법론을 활용하여 Lifetime과 마찬가지로 데이터 처리에 시간을 써서 Lifetime Revenue를 구하여 값을 계산할 수 있다. Retention의 형태와 반대로 Lifetime Revenue 지표는 초반에 변화가 크고 이후에는 매우 조금씩 “증가”하는 것이 일반적이고, 경험적으로 “로그 함수” 형태를 통해 증가한다.
분석에 해당하는 유저의 D0~30의 매출 데이터를 추출하고, 이를 누적으로 계산한 후 로그함수로 예측을 통해 D-700의 총 Lifetime Revenue를 계산할 수 있다. (여기선 D0~700의 합이 아닌 D700의 데이터 포인트가 구하고자 하는 값)
이제 평균 ARPU는 Lifetime Revenue에 AU 수 총합을 나누면 되는데, AU 수 총합은 4-1에서 구한 Lifetime에 분석에 사용된 총 유저수 (# of Day0 Users)를 곱하면 계산 가능하다.
하지만 스타트업에선 항상 시간이 부족하다.
사실 LTV는 정기적으로 기록하고 관리하고 있기 때문에, 분석 대상 기간에 유입된 유저들의 미리 계산되어있는 LTV 값에 Lifetime을 나누어서 역산하여 평균 ARPU를 구하였다. (Lifetime * x = LTV , x = LTV/Lifetime) 😋
4-3 LTV 시뮬레이션
신규유저냐 기존 유저냐 혹은 장기 유저냐에 따라 Retention의 변화를 측정할 수 있는 방법은 다양할 것이다. 분석의 맥락에선 주로 신규유저의 Retention 변화가 목적이었으므로 평균 ARPU를 고정값으로 두고 Day1 Retention 1%p 오를 때 LTV 변화를 시뮬레이션 범위로 좁혔다.
이 때 실측+예측해놓은 Day0~Day700 데이터에서 n_day retention과 (n+1)_day retention의 비율을 고정값으로 사용하여 최초 리텐션인 Day1 Retention 상승에 따른 LTV 변화를 시뮬레이션 했다. 예를 들어 Day1 Retention과 Day2 Retention의 비율은 0.6 이고 Day1 Retention이 10%에서 15%로 +5%p오르면 Day2 Retention이 6%에서 9%로 상승한 것으로 가정하는 것이다. (15% * 0.6 = 9%). 마찬가지로 700개의 n_day retention과 (n+1)_day retention의 비율을 수식을 활용해 고정값으로 구해놓았다.
그 후 Day1 Retention이 1%p 오르면 Day2~700의 Retention이 고정된 비율에 따라 자동적으로 계산되게끔 구성하고 이를 전부 더하여 Lifetime이 계산되도록 하였다.
Lifetime인 계산되면 여기에 평균 ARPU를 곱하면 LTV를 구할 수 있게 된다! Job done! 🙂
나는 이 시뮬레이션 결과를 통해 Day1 Retention이 +1%p~+20%p 상승하면 비즈니스에 미치는 영향이 어떠한지를 주요 의사결정자 분들께 설명할 수 있었다.
5. 한계점
- n_day retention과 (n+1)_day retention의 비율을 고정값으로 사용하여 최초 리텐션인 Day1 Retention 상승에 따른 LTV 변화를 시뮬레이션 했다. 하지만 현실은 똑같은 배율로 retention이 변화하진 않는다. 만약 서비스의 Day1 Retention을 집중 타겟한다면 유저의 Day2 경험은 건들이지 않아 Day1 Retention이 오른만큼 Day2 Retention이 기존과 똑같은 비율로 상승하지 않을 수 있다. 여기서 디자인한 방법론은 이러한 다이나믹한 변화를 캐치하지 못한다.
- 상승하는 Retention이 초기리텐션 / 중기리텐션 / 장기리텐션이냐에 따라 접근방법이 다를 것이다. 이 방법론은 초기리텐션을 타겟으로 한정한다.
6. 회고
- 사실 업무량이 많은 와중에 빠른시간 안에 시뮬레이션 해야 했고 처음 해보는 과제인지라 한낱 미생인 나에겐 challenge였던 과제였다. 하지만 많은 부분 상사인 Kenny(양승국 팀장님)께 가이드를 받으며 헤쳐나갈 수 있었고, 성장에 도움이 되었다고 체감했다. LTV에 대한 지표 이해력이 높아진 게 큰 수확. 이 글을 빌어 다시 한 번 감사 말씀드리고 싶다.
- 로직을 깊게 이해하고 실행하는 것은 아무리 엑셀로 했다지만 분석가 이외 포지션에서 수행하기 힘들 것으로 생각된다. 이를 고려해서 엑셀에서 자동 계산기처럼 사용할 수 있는 프레임을 만들어 놓고 다른 분들이 활용할 수 있게끔 세팅해 놓았다면 구성원들에게 더 좋은 평가를 받을 수 있지 않았을까 싶다.
