이 글은 작성자 블로그에서도 보실 수 있습니다.

• 이번 글에 있는 코드를 실행하기 위해 필요한 라이브러리를 먼저 설치해 주세요.

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import random

from scipy.stats import beta
from scipy.stats import binom

Markov Chain Monte Carlo 이해

[저번 글](https://yeonjuohh.github.io/data-analysis/bayesian_ab_test_bayes_theorem/“에서는 베이지안 접근 방식으로 A/B 테스트 결과를 해석해 보았습니다. Bayes’ theorem을 사용하면 사후 분포를 수리적으로 유도할 수 있어 사후 평균, 사후 분산 등을 쉽게 계산할 수 있습니다.

모든 문제에서 사후 분포를 계산할 수 있으면 좋겠지만 실제로는 분포가 복잡하거나 모수가 많아 어려운 경우가 더 많습니다. 이런 문제에서는 사후 분포로부터 랜덤 표본을 생성해, 표본의 수를 충분히 크게 함으로써 분포에 대한 추론을 할 수 있습니다.

사후 분포 $Beta(61,41)$의 평균과 분산을 식이 아닌 랜덤 표본을 이용해 계산해 보겠습니다. $Beta(61,41)$에서 10,000개의 랜덤 데이터를 추출하고 이 데이터의 평균과 분산을 계산합니다.

n_sample = 10000
samples = []

for idx in range(n_sample):
    samples.append(beta.rvs(61,41))

print(round(np.mean(samples), 4))
print(round(np.var(samples), 4))

0.5975
0.0023

$Beta$분포의 평균과 분산식을 이용하면 평균은 ${61\over{(61+41)}}=0.598$, 분산은 ${61\cdot41\over{(61+41)^2(61+41+1)}}=0.0023$으로 랜덤 표본으로 계산한 값과 거의 차이가 없습니다. 물론 이 문제에서는 사후 분포를 명확하게 알고 있기 때문에 굳이 표본을 이용한 근사가 필요하지는 않았지만 충분히 많은 표본을 뽑는다면 분포에 대한 추론을 상당히 정확하게 할 수 있다는 걸 확인했습니다.

MCMC(Markov Chain Monte Carlo)는 사후 분포를 근사적으로 추정하는 방법 중 하나로 다양한 문제에서 쉽게 적용할 수 있기 때문에 많이 사용되고 있습니다. 이름에서 알 수 있듯이 MCMC는 Markov Chain과 Monte Carlo를 기반으로 합니다. Monte Carlo는 특정 분포로부터 랜덤 데이터를 생성하는 시뮬레이션 방법이고, Markov Chain은 A 상태에서 B 상태가 될 때 B 상태는 오로지 A 상태에만 영향을 받는 확률 과정을 의미합니다. 즉, MCMC는 Markov Chain을 이용해 사후 분포로부터 샘플링을 얻고, 이 데이터로 사후 분포에 대한 추론을 하는 방법이라고 할 수 있습니다.

Metropolis-Hastings 알고리즘

Metropolis-Hastings는 MCMC의 대표적인 알고리즘입니다. 현재 값 $\theta_t$가 있다고 하겠습니다. Metropolis-Hasting에서는 $\theta_{t}$에서 다음 후보 값 $\theta_{t+1}$을 선택한 다음 $U(0,1)$에서 랜덤으로 뽑은 값이 $\alpha$보다 작으면 표본으로 채택하고, 크면 채택하지 않습니다. $\pi(\theta_{t}|x)$를 $\theta_t$가 나올 확률, ${q(\theta_{t+1}|\theta_{t})}$를 $\theta_{t}$가 주어졌을 때 $\theta_{t+1}$의 조건부 확률 분포라 하면 $\alpha$는 다음의 식으로 계산합니다.

${{\pi(\theta_{t+1}|x)} \over {\pi(\theta_{t}|x)}}$이 1보다 크다는 건 $\theta_{t+1}$이 나올 확률이 $\theta_t$이 나올 확률보다 크다는 걸 의미합니다. 이 값을 우도 함수의 비 ${{q(\theta_{t}|\theta_{t+1})} \over {q(\theta_{t+1}|\theta_{t})}}$로 보정하는 이유는 ${{\pi(\theta_{t+1}|x)} \over {\pi(\theta_{t}|x)}}$만을 사용하면 알고리즘 특성상 나올 확률이 높은 값으로 샘플의 수가 치중되기 때문입니다. 후보 값 $\theta_{t+1}$은 보통 대칭 분포에서 랜덤으로 추출하는데 $U(0,1)$ 또는 $N(\theta_t,\delta^2)$이 많이 사용됩니다.

정리하면 다음과 같습니다.

$\theta_t$가 있을 때

1. $U(0,1)$ 또는 $N(\theta_t,\delta^2)$에서 $\theta_{t+1}$를 랜덤으로 추출합니다.
2. $U(0,1)$에서 $u$를 랜덤으로 추출합니다.
3. $\alpha=min[1,{{\pi(\theta_{t+1}|x)} \over {\pi(\theta_{t}|x)}} \cdot {{q(\theta_{t}|\theta_{t+1})} \over {q(\theta_{t+1}|\theta_{t})}}]$를 계산합니다.
4. $u<\alpha$면 $\theta_{t+1}$을 채택하고, $u>\alpha$면 채택하지 않습니다.

$\theta_{t+1}$는 $\theta_1,...,\theta_{t-1}$와 아무런 관련이 없다는 걸 확인할 수 있습니다. 즉, $\theta_{t+1}$는 바로 이전 값인 $\theta_{t}$에만 영향을 받는 Markov Chain의 특징을 가지고 있습니다. 위 과정을 충분히 반복해 많은 $\theta$를 얻으면 타겟 분포에 수렴하게 됩니다.

A/B 테스트에 MCMC 적용하기

전환율을 비교하는 실험에서 실험군과 대조군에 각각 유저가 100명씩 들어왔고, 실험군에서는 60명 대조군에서는 65명이 전환되었다고 하겠습니다. 전환율에 대해 알고 있는 정보가 아무것도 없기 때문에 사전 분포로는 $Beta(1, 1)$, $\theta$가 0에서 1사이의 값을 가지고 일어날 수 있는 이벤트는 두 가지(이벤트를 발생시키거나 안 하는) 중 하나이기 때문에 우도 함수로는 이항분포를 사용합니다. 저번 글 내용을 참고하면 실험군의 사후 분포는 $Beta(60+1, 100-60+1)=Beta(61,41)$, 대조군의 사후 분포는 $Beta(65+1,100-65+1)=Beta(66, 36)$라는 걸 쉽게 계산할 수 있습니다.

하지만 어떠한 이유로 인해 사후 분포를 쉽게 구하지 못하는 상황에 처해 MCMC 방법을 활용해 사후 분포로부터 표본을 추출해 보기로 하겠습니다. 사전 분포와 우도 함수를 계산하는 prior, likelihood 함수를 정의합니다.

def prior(a, b, p):
    return beta.pdf(p, a, b)

def likelihood(n, x, p):
    return binom.pmf(x, n, p)

Metropolis-Hastings 알고리즘을 사용해 사후 분포로부터 표본을 생성합니다. 후보 값 $\theta_{t+1}$은 $U(0,1)$에서 추출합니다.

# 사전 분포 모수
a = 1
b = 1

# 우도 함수 모수
n = 100
x = 60

# 샘플 데이터 총 겟수
n_samples = 100000
theta_samples = []

theta_t = np.random.uniform(0, 1, 1)[0]  # initialization
for idx in range(n_samples):
        # U(1,1)에서 후보 값 추출
    theta_t_1 = np.random.uniform(0, 1, 1)[0]
    
        # U(1,1)에서 u 추출
    u = np.random.uniform(0, 1, 1)[0]
    
        # alpha 계산
    alpha = min(
        1, 
        (prior(a, b, theta_t_1) / prior(a, b, theta_t)) 
        * (likelihood(n, x, theta_t_1) / likelihood(n, x, theta_t)))

        # alpha와 u를 비교해 alpha가 u보다 크면 후보 값을 채택
    if u < alpha:
        theta_samples.append(theta_t_1)
        theta_t = theta_t_1

생성 된 표본으로 밀도 함수를 그려보았습니다.

x = np.linspace(0, 1, 500)

control = []
for x_v in x:
    control.append(beta.pdf(x_v, 61, 41))
    
plt.figure(figsize=(10, 8))

plt.plot(x, control, label='true')
sns.kdeplot(theta_samples_1000, label='1,000 samples')
sns.kdeplot(theta_samples_100000, label='100,000 samples')

plt.legend()

plt.show()

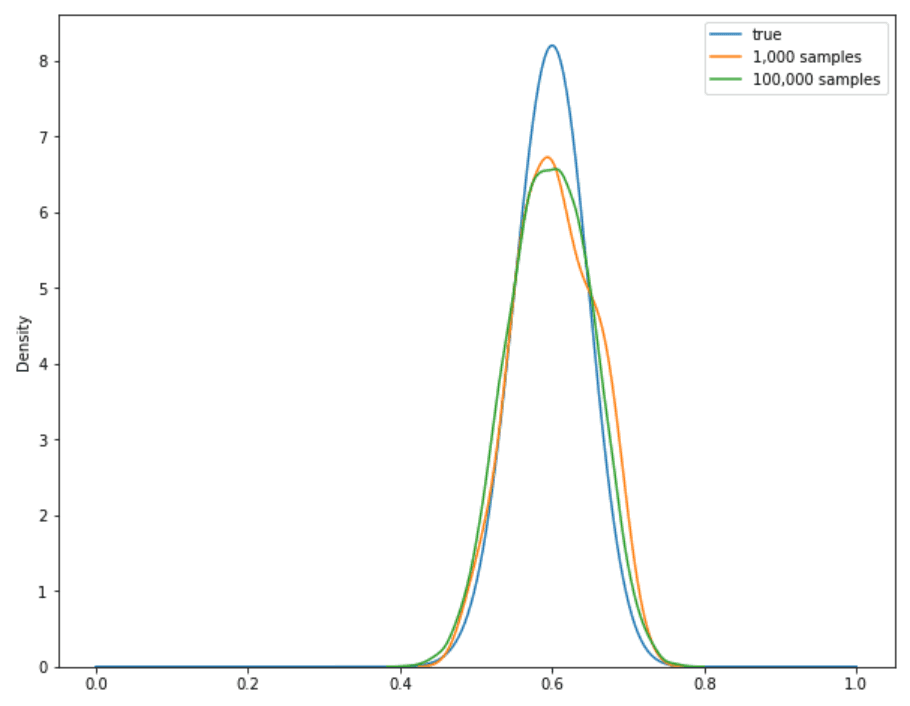
n_samples이 1,000일 때와 100,000일 때 함수의 모양을 비교해 보았습니다. 표본의 수가 많아질수록 $Beta(61,41)$ 분포 모양에 수렴하는 걸 확인할 수 있습니다.

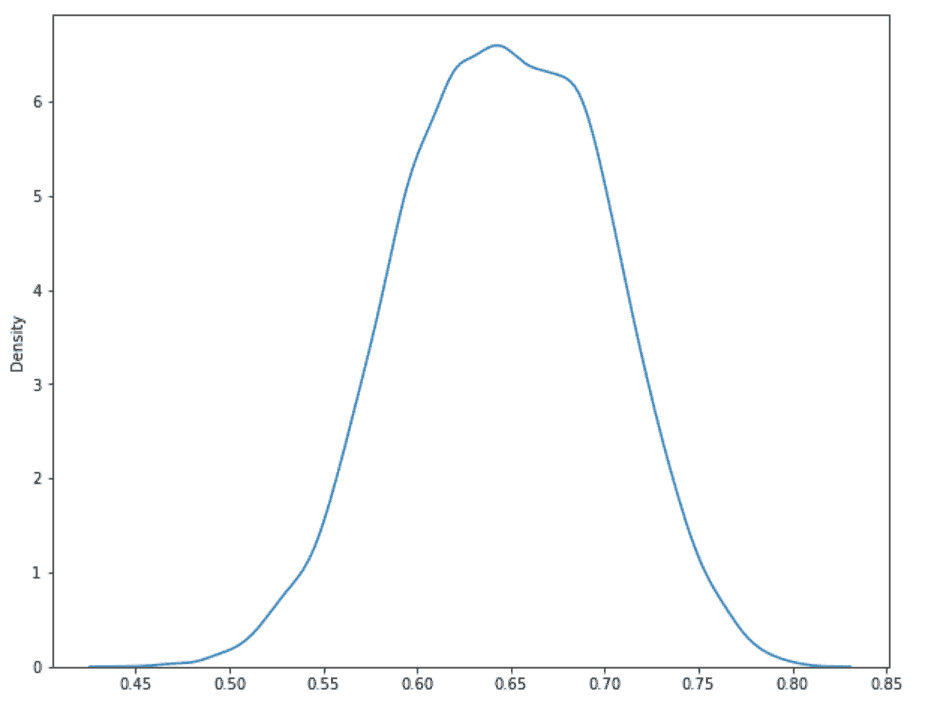
같은 방법으로 우도 함수의 모수만 수정해 대조군의 사후 분포 밀도 함수도 그려보았습니다.

print(round(np.mean(theta_samples), 4))
print(round(np.var(theta_samples), 4))

0.6033
0.0027

$Beta$ 분포의 평균과 분산 공식을 사용하면 실험군 사후 분포 $Beta(61,41)$의 평균은 0.598, 분산은 0.0023입니다. 사후 분포로부터 표본을 더 많이 생성할수록 참값에 더 가까워질 것 입니다.

실험군의 CTR이 대조군의 CTR보다 클 확률을 계산해 보겠습니다.

n_sample = 10000
v = 0

for idx in range(n_sample):
    if random.sample(theta_c_samples, 1) < random.sample(theta_t_samples, 1):
        v += 1

print(v / n_sample)

실험군과 대조군의 사후 분포 표본에서 값을 하나씩 랜덤으로 추출하고 크기를 비교합니다. 10,000번 반복했을 때 대보군에서 추출한 값이 더 큰 경우가 7,291번 있었습니다. 즉, 대조군의 CTR이 실험군의 CTR보다 클 확률은 0.7291입니다.

• 개인이 공부한 내용을 정리했기 때문에 오류가 있을 수 있습니다. 혹시 발견하신다면 메일로 알려주세요. 감사합니다 :)