베이지안 A/B 테스트

Home About

Experiment

베이지안 A/B 테스트 - Bayes theorem

오연주

June 06, 2022

3 min

빈도주의(Frequentist) vs 베이지안(Bayesian)

베이지안 A/B 테스트

이 글은 작성자 블로그에서도 보실 수 있습니다.

빈도주의(Frequentist) vs 베이지안(Bayesian)

A/B 테스트 결과를 빈도주의(Frequentist) 방법으로 해석하려면 p-value가 필요합니다. P-value는 실험군과 대조군간에 차이가 없다는 귀무가설이 참이라고 했을 때 실험을 통해 관찰된 데이터보다 더 극단적인 데이터가 나올 확률인데, 이 값이 작다는 건 귀무가설이 맞다는 가정하에 나오기 힘든 데이터를 얻었다는 의미입니다. 보통 p-value가 유의 수준(1종 오류)보다 작으면 귀무가설을 기각하고, 실험군과 대조군간에 차이가 있다는 결론을 내립니다.

빈도주의 방법의 가설 검정은 자주 사용되지만 몇 가지 단점이 있습니다. 대표적으로 2종 오류보다 1종 오류를 더 심각하게 간주하기 때문에 가능하면 귀무가설을 기각하지 않으려고 합니다. 그렇기 때문에 주의하지 않으면 귀무 가설과 대립 가설을 어떻게 정의하느냐에 따라 검정 결과가 달라질 수 있기도 하고, 2종 오류를 더 심각하게 봐야 하는 문제에서는 적용하기 어렵습니다.

빈도론자들은 확률을 장기적으로 일어난 사건의 빈도라고 정의합니다. 예를 들어, 동전을 던졌을 때 나올 수 있는 경우의 수는 2개이기 때문에 실험을 무한히 반복하면 앞이 나오는 확률은 $1/2=0.5$ 입니다. 또한, 모집단의 평균, 분산 등 우리가 알고 싶은 모수를 고정된 상수라 여깁니다.

베이지안(Bayesian)론자들은 모수는 확률적으로 변하는 값이라고 생각합니다. 베이지안에서는 동전을 던졌을 때 나올 수 있는 경우의 수가 2개라고 해도 앞이 나올 확률은 $0.5$ 가 아닐 수 있습니다. 실제로 동전을 100번 던져보았는데 앞이 55번 나왔다면 앞이 나올 확률은 $0.55$ 입니다. 또한, 베이지안에서 모수는 고정된 상수가 아니라 분포이기 때문에 앞이 나올 확률이 $0.55$ 라는 것보단 앞이 나올 분포를 더 궁금해합니다.

베이지안 검정은 귀무 가설과 대립 가설을 구분하지 않고 실험으로 얻은 데이터로 실험군과 대조군의 분포를 추정하기 때문에 빈도주의 가설 검정이 가지고 있는 한계를 보완해 줄 수 있습니다. 또한, 신뢰성 있는 실험 결과를 얻기 위해 필요한 데이터 수가 빈도주의 가설 검정보다 작기 때문에 많은 데이터를 확보하기 어려운 실험에서 유용하게 사용되고 있습니다.

Bayes’ theorem

Bayesian은 통계학을 공부했다면 한 번쯤은 보았을 Bayes’ theroem를 토대로 합니다.

P(B|A)={P(A|B)P(B)\over P(A)}

위 공식을 A/B 테스트에 적용하면, 다음과 같이 정리할 수 있습니다.

P(\theta|x)={P(x|\theta)P(\theta) \over P(x)}

실험으로 알고 싶은 건 왼쪽에 있는 $P(\theta|x)$ 로 실험 데이터가 주어졌을 때 $\theta$ 의 확률입니다. 이를 사후 확률(posterior probability)이라 합니다. 오른쪽 분모에 있는 $P(x)$ 는 $\theta$ 계산에 필요 없기 때문에 식은 더 간단히 나타낼 수 있습니다.

P(\theta|x)\propto P(x|\theta)P(\theta)

$P(\theta)$ 는 아무런 데이터가 없을 때 $\theta$ 의 분포로 사전 확률(prior probability)이라 합니다. $P(x|\theta)$ 는 $\theta$ 가 주어졌을 때 실험 데이터를 얻을 확률로 가능도(likelihood)라 합니다. 즉, 사후 확률은 사전 확률과 가능도 곱에 비례합니다.

A/B 테스트에 Bayes’ theorem 적용하기

실험군과 대조군의 CTR을 비교하는 A/B 테스트를 예를 들어 Bayes’ theorem을 A/B 테스트에 어떻게 적용할 수 있을지 살펴보겠습니다.

가장 먼저 해야 할 일은 실험을 통해 알고 싶은 $\theta$ , CTR의 사전 분포를 정의하는 것입니다. 사전 분포로는 사후 분포 추정을 쉽게 할 수 있는 베타 분포(Beta distribution), 포아송 분포(Poisson distribution), 정규 분포(Normal distribution) 등이 주로 사용됩니다. 만약 CTR 관련해서 사전 정보를 알고 있다면 활용할 수 있지만, 지금은 아무것도 알 수 없는 상태이기 때문에 0에서 1 사이의 값을 가지고 어떤 값이든 나올 확률이 같은 $Beta(1, 1)$ 를 실험군과 대조군의 사전 분포로 선택하겠습니다. $Beta(1, 1)$ 를 정리해 보면 $U(0, 1)$ 와 같습니다.

f(x|1,1)={\Gamma(\alpha+\beta) \over \Gamma(\alpha)\Gamma(\beta)} x^{\alpha-1}(1-x)^{\beta-1} \\ = {\Gamma(2) \over \Gamma(1)\Gamma(1)}x^{0}(1-x){0} \\ = 1

$\theta$ 는 0에서 1사이의 값을 가지고, 유저가 들어와서 할 수 있는 행동은 두 가지(이벤트를 발생시키거나 안 하는) 중 하나이기 때문에 $P(x|\theta)$ 는 이항분포를 따른다고 할 수 있습니다.

실험을 시작하니 100명의 유저가 실험군에 들어와 이 중 60명이 이벤트를 발생시켰습니다. 이제 사후 분포를 추정해 볼 건데, 여러 가지 방법이 있지만 이번 글에서는 Bayes’ theorem을 활용해보겠습니다.

P(\theta_{c}|x) \propto P(x|\theta_{c})P(\theta_{c}) \\=\binom {100} {60}\theta_{c}^{60}(1-\theta_{c})^{100-60} {\Gamma(2) \over \Gamma(1)\Gamma(1)} x^{0}(1-x)^{0} \\ = \binom {100} {60}\theta_{c}^{60}(1-\theta_{c})^{100-60} \\ \propto \theta_{c}^{60+1-1}(1-\theta_{c})^{100-60+1-1} \\ \sim Beta(60+1, 100-60+1)

사후 분포도 사전 분포처럼 베타 분포를 따르는 걸 확인할 수 있습니다. 사전 분포로 베타 분포를 사용하면 사후 분포를 어려움 없이 계산할 수 있어 자주 사용되는데, 이와 같이 사후 분포가 사전 분포와 같은 분포를 따르게 되는 사전 분포를 공액 사전 분포(conjugate prior distribution)라 합니다. 위 식을 정리하면 다음과 같이 나타낼 수 있습니다.

P(\theta|x)=\binom {n} {x}\theta^{x}(1-\theta)^{n-x} {\Gamma(\alpha+\beta) \over \Gamma(\alpha-1)\Gamma(\beta-1)} x^{\alpha-1}(1-x)^{\beta-1} \\ \propto \theta^{x+\alpha-1}(1-\theta)^{n-x+\alpha-1} \\ \sim Beta(x+\alpha, n-x+\beta)

대조군에서 결과를 살펴보니 실험에 들어온 100명 중 65명이 이벤트를 발생시켰습니다. 굳이 계산하지 않고 위 식을 활용해보면 대조군의 사후 분포는 $Beta(65+1, 100-65+1)$ 라는 걸 쉽게 알 수 있습니다.

여기서 실험을 정지하고 결과를 볼 수 있지만 더 많은 데이터를 활용하기 위해 추가 실험을 진행했다고 하겠습니다. 대조군과 실험군에 각각 100명의 유저가 추가로 유입되었고 실험군에서는 40명, 대조군에서는 60명이 이벤트를 발생시켰습니다. 위에서 정리한 식을 또 다시 활용하면 실험군 CTR의 사후 분포는 $Beta(60+1+40+1, 100-60+1+100-40+1)$ , 대조군 CTR의 사후 분포는 $Beta(65+1+60+1, 100-65+1+100-60+1)$ 입니다.

Python으로 실험군과 대조군의 사후 분포 그래프를 그려보겠습니다. 그래프를 보면 대조군의 CTR이 실험군보다 더 높다는 걸 확인할 수 있습니다.

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import beta

x = np.linspace(0, 1, 500)

control = []
treatment = []
for x_v in x:
    control.append(beta.pdf(x_v, 102, 102))
    treatment.append(beta.pdf(x_v, 127, 77))

plt.figure(figsize=(10, 8))

plt.plot(x, control, label='Control')
plt.plot(x, treatment, label='Treatment')

plt.legend()

plt.show()

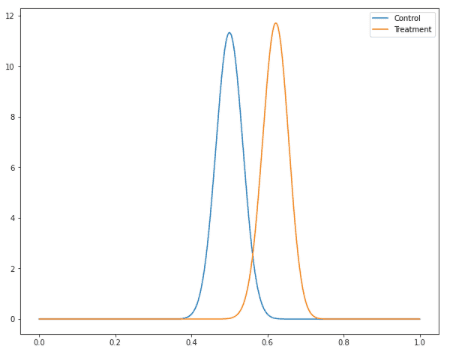
베타 분포의 평균과 분산을 구하는 식을 활용하면 사후 분포의 평균과 분산도 계산할 수 있습니다. 대조군의 평균과 분산은 다음과 같습니다.

E(X)={\alpha \over \alpha+\beta}={127 \over 127 + 77}=0.6225\\ Var(X)={\alpha\beta \over (\alpha+\beta)^2(\alpha+\beta+1)} = { 127 * 77 \over (127 + 77)^2(127+77+1)}=0.0011

사후 분포 그래프로 우리는 대조군의 CTR이 실험군보다 더 좋다는 걸 확인했습니다. 하지만, 두 그래프가 겹쳐지는 부분이 있기도 하고 우연히 나온 결과일 수도 있기 때문에 그래프만 보고 결론을 내리기에는 위험합니다. 베이지안에서는 이런 상황에서 대조군이 실험군 보다 크거나 작을 확률을 계산할 수 있습니다. 이를 식으로 나타내면 다음과 같습니다.

P(\theta_{t}>\theta_{c})=\int_{0}^{1}\int_{\theta_{c}}^{1}P(\theta_{t}|x)P(\theta_{c}|x)d\theta_{t}d\theta_{c}

Python Scipy 라이브러리의 dblquad 함수를 이용해 적분을 계산하겠습니다.

from scipy import integrate

def f(t, c):
    return beta.pdf(t, 127, 77) * beta.pdf(c, 102, 102)

p, err = integrate.dblquad(
    func=lambda t, c: beta.pdf(t, 127, 77) * beta.pdf(c, 102, 102),
    a=0,
    b=1,
    gfun=lambda c: c,
    hfun=lambda c: 1,
    epsabs=1.498e-8
)

print(p)

위 코드를 실행하면 결괏값으로 0.99가 나오는데, 이는 대조군의 CTR이 실험군의 CTR보다 높을 확률이 0.99라는 걸 의미합니다. 이제 조금 더 자신 있게 대조군의 CTR이 높을 확률이 더 높다는 결론을 내릴 수 있습니다. 보통 확률이 0.9 이상이면 충분히 높다고 판단합니다.

만약, 추가 실험에서 대조군에 새로 들어온 100명의 유저 중 60명이 아닌 50명만 이벤트를 발생시켰다면, 대조군 CTR이 실험군 CTR보다 높은 확률은 0.93으로 값이 작아집니다.

베이지안 A/B 테스트의 장점을 알아보고, A/B 테스트에 Bayes’ theorem을 적용해 보았습니다.

모든 문제에서 공액 사전 분포를 사용해 사후 분포를 쉽게 추정할 수 있으면 좋겠지만 현실은 그렇지 않습니다. 이때는 랜덤 샘플을 추출해 사후 분포를 추정하는 MCMC(Markov chain Monte Carlo)를 사용해 문제를 해결할 수 있습니다. 다음 글에서는 MCMC에 대해 간략히 알아보고, A/B 테스트에 적용해 보겠습니다.

개인이 공부한 내용을 정리했기 때문에 오류가 있을 수 있습니다. 혹시 발견하신다면 메일로 알려주세요. 감사합니다 :)

Table Of Contents

빈도주의(Frequentist) vs 베이지안(Bayesian)